If you are training to be good at any sport then you are in the
business of optimisation - doing all you can to enhance anything
that will make you do better and minimise any faults that hinder
your performance. This is one of the areas of sports science that
relies on the insights that are possible by applying a little bit
of mathematics. Here we are going to think about two athletics
events where you try to launch the body over the greatest
possible height above the ground: high jumping and pole vaulting.
This type of event is not as simple as it sounds. Athletes must
first use their strength and energy to launch their body weight
into the air. If we think of a high jumper as a projectile of
mass M launched vertically upwards at speed $U$ then the height
$H$ that can be reached is given by the formula $$U^{2}=2g H$$
where $g$ is the acceleration due to gravity. Alternatively we
can think in terms of energy conservation. The kinetic energy of
the jumper at take-off is $\frac{1}{2}M U^{2}$ and this will be
transformed into the potential energy $M g H$ gained by the
jumper at the maximum height $H$ when he is instantaneously at
rest at the highest point. Equating the two gives $ U^{2}=2g H$
again. All this sounds straightforward but the tricky point is
the quantity $H$ - what exactly is it? It is not the height that
is cleared by the jumper. Rather, it is the height that the
jumper's centre of gravity is raised, and that is rather a subtle
thing because it makes it possible for a high jumper's body to
pass \emph{over} the bar even though his centre of gravity passes
\emph{under} the bar. When an object has a bendy shape it is
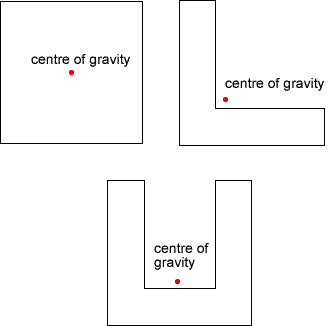
possible for its centre of gravity to lie outside of the body.One
way to locate the centre of gravity of an object is to hang it up
from one point and drop a weighted string from any point on the
object, mark where the string drops. Then repeat this by hanging
the object up from another point. Draw a second line where the
hanging string now falls. The centre of gravity is where the
lines of the two strings cross. If the object is a square then
the centre of gravity will lie at the geometrical centre but if
it is L-shaped or U-shaped the centre of gravity will not lie
inside the boundary of the body at all.
It is this possibility that allows a high jumper to control where
his centre of gravity lies and what trajectory it follows when he
jumps. The aim of our high-jumper is to get his body to pass over
the bar whilst making his centre of gravity pass as far
underneath the bar as possible. In this way he will make optimal
use of his explosive take-off energy. The simple high-jumping
technique that you first learn at school, called the 'scissors'
technique is far from optimal. In order to clear the bar your
centre of gravity, as well as your whole body, must pass over the
bar. In fact your centre of gravity probably goes close to 30
centimetres higher than the height of the bar. This is a very
inefficient way to clear a high-jump bar. The high-jumping
techniques used by top athletes are much more elaborate. The old
'straddle' technique involved the jumper rolling around the bar
with their chest always facing the bar. This was the favoured
technique of world-class jumpers up until 1968 when the American
Dick Fosbury amazed everyone by introducing a completely new
technique which involved a backwards flop over the bar and won
him the Gold Medal at the 1968 Olympics in Mexico City. This
method was only safe when inflatable landing areas became
available. Fosbury's technique was much easier for high jumpers
to learn than the straddle and it is now used by every serious
high jumper. It enables a high jumper to send their centre of
gravity well below the bar even though their body curls over and
around it. The more flexible you are the more you can curve your
body around the bar and the loweryour centre of gravity will be.
The 2004 Olympic men's high-jump champion Stefan Holm, from
Sweden, is rather small by the standards of high jumpers but is
able to curl his body to a remarkable extent. His body is very
U-shaped at his highest point. He sails over 2m 37 cm but his
centre of gravity goes well below the bar.
The photographer Peter Kjelleras captures the Olympic
high-jump champion Stefan Holm jumping at the World Athletics
Championships in Paris, in 2003. Holm dramatically demonstrates
his ability to send his centre of gravity far below the bar he is
clearing 2.32 metres above the ground.
The high-jumper's centre of mass is about two-thirds of the way up his body
when he is standing or running in towards the take off point. He needs to
increase his launch speed to the highest possible by building up his
strength and speed, and then use his energy and gymnastic skill to raise his
centre of gravity by
, which is the maximum that the formula
will allow. Of course there is a bit more to it in practice!
When a high jumper runs in to launch himself upwards he will only be able to
transfer a small fraction of his best possible horizontal sprinting
speed into his upward launch speed. He has only a small space for his
approach run and must turn around in order to take off with his back facing
the bar. The pole vaulter is able to do much better. He has a long straight
run down the runway and, despite carrying a long pole, the world's best
vaulters can achieve speeds of close to
metres per second at launch.
The elastic fibre glass pole enables them to turn the energy of their
horizontal motion
into vertical motion much more
efficiently than the high jumper. Vaulters launch themselves vertically
upwards and perform all the impressive gymnastics necessary to curl
themselves in an inverted U-shape over the bar,sending their centre of
gravity as far below it as possible.
Let's see if we can get a rough
estimate of how well we might expect them to do. Suppose they manage to
transfer all their horizontal running kinetic energy of
into vertical potential energy of
then thy will raise their centre of
mass a height of:
If the Olympic champion can reach
launch speed then since the
acceleration due to gravity is
we expect him to be able to
raise his centre of gravity height of
metres. If he started with his
centre of gravity about
metres above the ground and made it pass
metres below the bar then he would be expected to clear a bar height of
metres. In fact, the American champion Tim Mack won the Athens
Olympic Gold medal with a vault of
metres (or
in feet and inches) and had three very close failures at
metres,
knowing he had already won the Gold Medal, so our very simple estimates turn
out to be surprisingly accurate.
John D. Barrow is Professor of Mathematical Sciences and Director of
the Millennium Mathematics Project at Cambridge University.