Curt from Reigate College started by getting a general formula for Triangle numbers

$T_n = 1 + 2 + 3+ . . . +(n-1) + n$

$T_n = n + (n-1) + . . . + 3+2+1$

The second line is just a repeat of the first but with the terms in reverse order.

Then adding the two lines the right hand side becomes $n$ lots of $n+1$

So $2T_n=n(n+1)$\par and since everything was added in twice,

$T_n=\frac{n(n+1)}{2}.

David from Sha Tin College used a known general result for any progression that steps up by a fixed amount term on term

$\frac{n}{2}(2a+(n-1)d)$

where n is the number of terms, a is the starting term and d is that step up.

If the step up is equal to 1, and the start value is also 1, you can see that this is the same result as Curt demonstrated.

Continuing with the Pentagonal numbers

The diagram shows $P_4=3T_3+4$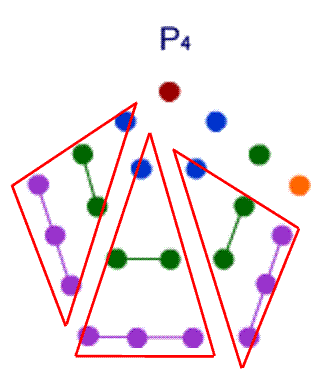pentagonal arrangement
And in general Pn=3Tn-1+n


Now using the result for Tn to see Pn in terms of n


Pn= 3n(n-1)
2
 +n


We now have to show that three times that result is a triangle number



3Pn=3[ 3n(n-1)+2n
2
 ]

and is the same as
3[ 3n2-n
2
 ]


or



3n(3n-1)
2


And that's the same as T3n-1 the required result