By Pythagoras Theorem:

|AB|=Ö3, |BC|=Ö2, |AC|=Ö5, |BD|=Ö5, |AD|=Ö10.

As |AB|² + |BC|² = |AC|² it follows, by the converse of Pythagoras Theorem, that ÐABC = 90^o.

Using the cosine rule: |AD|² = |AB|² + |BD|² - 2|AB||BD|cosB. So

cosB = -1 Ö15

and ÐABD = 105 degrees to the nearest degree.

The challenge was to find more than one method so the second method uses geometry and vectors.

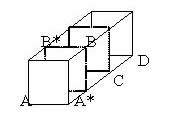
Triangle A*BC is a right angled isosceles triangle and A*B is perpendicular to BC.The line B*B is perpendicular to the plane A*BDC so it is perpendicular to BC. As the two line A*B and B*B are perpendicular to BC the whole plane AB*BA* is perpendicular to BC. Hence AB is perpendicular to BC.

Using vectors :

® BA   =(-1,-1,-1),  ® BD   =(2,0,-1).

So we find the scalar product:

® BA   . ® BD   = |BA||BD|cosB

which gives

-2+1 = Ö3 Ö5 cosB.

Again:

cosB = -1 Ö15

and ÐABD = 105 degrees to the nearest degree.