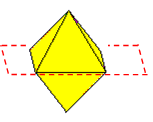
Think in 3D of a flower made from regular octahedra with the
vertices of the octahedra meeting at a point and faces in
contact. How many octahedra can be joined together in this way
around one centre?
Here is a solution from Andrei of Tudor Vianu National College,
Bucharest, Romania.
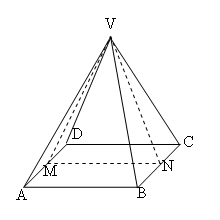
First, I observe that the octahedron is symmetrical about a plane
that passes through the 4 coplanar vertices (see figure), so for
the problem I may take into account only a pyramid.
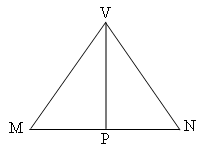
I shall calculate angle $MVN$.
As all exterior sides have equal lengths, without loss of
generality I may assume $AB = 1$. In this case $VN$ is the height
of equilateral triangle $VBC$, so it has a length of $\sqrt 3
/2$. $MN$ is equal to $AB$, having a length of 1.
To calculate angle $MVN$, I shall calculate its sine.
The angle at MVN (to 3 decimal places) is
Alternatively you could calculate this angle as
The number of octahedra is 360/70.529 = 5.1.
So 5 tetrahedra could be joined together in this way.