When you cut a square off a golden rectangle you are left with another rectangle whose sides are in the same ratio. In the diagram below, if you remove the orange square from rectangle AEFD, you are left with the yellow rectangle whose sides are in the same ratio as AEFD.

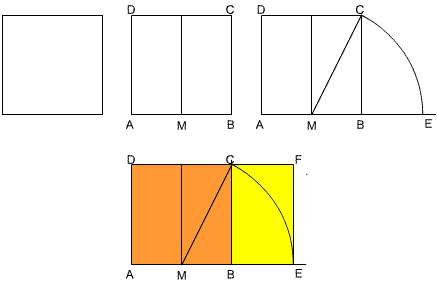
(1) Follow the instructions for drawing the rectangle AEFD. You can make the most accurate drawing by using a ruler and compasses. Draw a square ABCD of side length 10 cm. Bisect AB at M and draw an arc of radius MC to meet AB produced at E. If you prefer you can just measure MC and mark E on AB so that ME=MC. Draw EF perpendicular to AB to meet DC produced at F.

Measure AE and BE. From your measurements calculate the ratios AE/AD and BC/BE. What do you notice?

(2) Calculate the exact lengths of MC, AE and BE. Calculate the exact value of the ratios AE/AD and BC/BE and prove that they are equal. [Note: To get exact values you must work with surds and you will not be able to use a calculator.]

(3) Suppose this ratio is denoted by f and take 10 cm as 1 unit then AE is f units. Show that BE is 1/f units and hence

f = 1 + 1 f     (1)

Explain just from equation (1), and without solving the equation, why the equation must have a solution between 1 and 2.

(4) Draw the graphs of y=x, y=1/x and y=1+1/x on the same axes and use your graph to find an approximate value for f.

(5) Solve equation (1) to find the value of f.