Thank you to all who sent in solutions to
this problem. A lot of you sent in very careful answers to the
first 10 words of the sheep talk sequence. Well done to those of
you who also spotted the famous sequence of numbers involved,
including Richard aged 8 and Kevin aged 10.
Here is the solution sent in by Alistair of
Histon and Impington School:
A
B
AB
BAB
ABBAB
BABABBAB
ABBABBABABBAB
BABABBABABBABBABABBAB
ABBABBABABBABBABABBABABBABBABABBAB
BABABBABABBABBABABBABABBABBABABBABBABABBABABBABBABABBAB
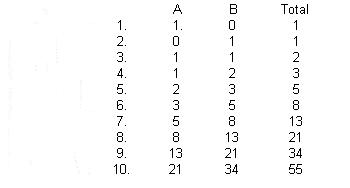
I noticed all the totals are Fibonacci numbers and the A
column is what the B column was last row, and the B column is
what the total used to be in the last row. I predict the next
numbers will be:

This is because the A's come from the B's in the previous row
and the B's come from the A's and B's (the total) in the previous
row.
This may be helpful:
Let an and bn be the number of A's and B's respectively in the
nth word and fn the total number of letters in the nth word.
Note that in each word there is an A for every B in the previous word
so
The number of B's is given by the number
of B's in
the previous word plus the number of A's in the previous word and so
.
Putting these two expressions together and substituting for an in (2)
we get
so the sequence bn is a
Fibonacci sequence and the pattern will continue. Similarly
substituting for bn in (2) we get
so the an forn a Fibonaci sequence
and the pattern will continue.
Because the two sequences of numbers are the same apart from the
shift of one place the total number of letters is also a Fibonacci
sequence pattern will continue.
|
|
| |
|
= an + bn = bn-1 + bn = bn+1 |
| |
|
= an-1 + bn-1 = an-1 + an = an+1 |
| |
| = an+1+ bn+1 = fn-1 + fn . |
|
|