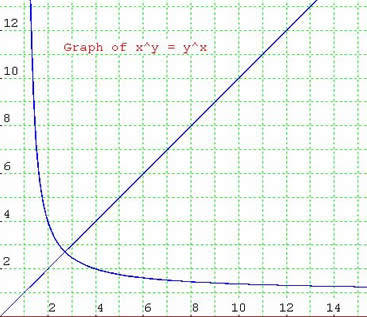
All points on the line y=x except the point (0,0) lie on the
graph but the function is not defined at the origin.
From the equation we see that the graph is symmetrical about the
line y=x because interchanging x and y in the equation
produces the same equation so that if (a,b) satisfies the
equation then (b,a) also satisfies the equation.
For x > 1 each line y=k for k £ e cuts the graph of
y=x1/x in two points (a, a1/a) and (b,b1/b) such
that a1/a=b1/b or, equivalently, ab=ba. Hence the two
points (a,b) and (b,a) are on the graph of xy=yx. For
example 24=42 so (2,4) and (4,2) are on the graph of
xy=yx.
The maximum point of the graph of y=x1/x is the point
(e,e1/e) so the point (e,e) lies on the graph of xy=yx.