Here is an operation table for the operation **.

**	0	1	2	3

0	0	0	0	0
1	0	1	2	3
2	0	2	1	0
3	0	3	0	0

Here are some examples of what the table tells us:

3**0

=

0
3** 1

=

3
2**2

=

1

We say that this set is "closed" for the operation **because the answer to any calculation involving two numbers in the set and ** is still in the set.
This means I can keep using and always get an answer in the set.
This operation is also symmetric and it has an identity element of 1 (an identity element does not change the other elements of the set when it operates on them)

1**0

=

0
1**1

=

1
1**2

=

2
1**3

=

3

We now have a closed set with an operation that is symmetric and we have an identity element.
Make up an operation table for addition modulo 4.

Think of this as adding numbers around a clock with only the times 0,1,2 and 3 o'clock - when you add 3 to 3 you get the answer 2 because you move around the clock three "hours" from 3 - landing on 2 (the remainder when you divide 6 by 4).
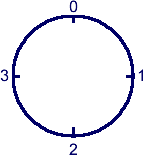
Clock with the numbers 0,1,2 and 3 around it

Does it have the same properties as the operation ** above?
Can you identify an identity element? Is it symmetric?

For more information on modulo arithmetic - look in the thesaurus.

What about subtraction and division mod 3 ?
Are addition modulo 3 and multiplication modulo 3 on this set associative?
Are they distributive over each other?

The terms associative and distributive are explained in the thesaurus.