This problem builds on the ideas described in the Symmetries article.
An equilateral triangle has a three-fold axis of symmetry,
which means the shape can fit onto itself three times in a full turn.
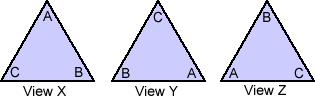
We can think of the three positions or views of the triangle as
the result of three different rotations of
0°, 120° and 240°.
We can name each of the three rotations and the views of the positions
of the triangle after each one:
E : turning clockwise 0° (no change) - gives View X
R1: turning clockwise 120° - gives View Y
R2: turning clockwise 240° - gives view Z
You might like to use the interactivity to check for yourself
that the table for the rotations will be the same as the one for the triquetrum.
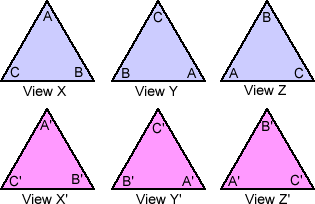
But with the equilateral triangle reflections in the altitudes
will also map the triangle onto itself.
An equilateral triangle has three altitudes and therefore three
planes of reflectional symmetry. Each through one of the three vertices.
Let's call them:
MA a reflection in the line of symmetry through the vertex at A - gives View X'
MB a reflection in the line of symmetry through the vertex at B - gives View Z'
MC a reflection in the line of symmetry through the vertex at C - gives View Y'
This means that we have six, not three, ways the triangle can fit onto itself:
Can you draw up a table of the effects of one reflection followed by another?
What do you notice and can you explain why?
Now can you complete the table for any combination of two operations (
rotation followed by rotation, rotation by reflection, reflection by rotation
and so on).
Can you explain any patterns you see in the operations table?