The fascinating model described in this article was created by Augustus M\"obius (1790 - 1868), a German mathematician and astronomer.

Here is a limerick describing the properties of the M\"obius band:

"A mathematician once confided
Old M\"obius' band is always one sided
If you want a good laugh
Cut the band in half
Notice, it stays in one piece when divided.''
(Source unknown)

You need:

$\bullet$ four long strips of paper, strips of A3 about 30mm wide are ideal.

$\bullet$ to draw in a centre line along each strip.

$\bullet$ some glue or sellotape and a pair of scissors.

Model A : Take a strip and glue the ends together.

Model B : Take a strip and at one end make a half twist ($180^{\circ}$). Glue the ends together.

Model C : Take a strip, at one end make a full twist ($360^{\circ}$). Glue the ends together.

Model D : Take a strip, at one end make three half twists ($540^{\circ}$). Glue the ends together.

Take each model in turn. Examine it carefully. Predict what will happen when a cut is made along the centre line.

Cut your models and record your results in the table below:

MODEL	NO. OF TWISTS	CUTTING PRODUCES	DESCRIPTION
A	0	2 separate strips	half width/same length
B	1/2
C	1
D	1 1/2

Can you predict what `shape' results for any number of half twists?

What about 6 half twists? 10 half twists?

You might like to investigate models based on a M\"obius strip which has two or more lines to cut along.

What next? ...

This work on the M\"obius band can be followed by an investigation into Euler's law.

Leonhard Euler (1707 - 1783), was a Swiss mathematician who is possibly best remembered for a rule he found that worked equally well with networks and polyhedra.

A network is a collection of vertices (dots) connected by arcs (lines) that create regions (spaces) in between.

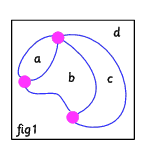
This network has 3 nodes, 5 arcs and 4 regions. The outside is counted also.

Study the networks below and complete the table

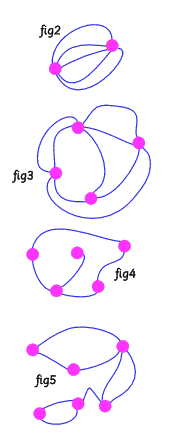
FIGURE	NODES	REGIONS	ARCS
1	3	4	5
2
3
4
5

\begin{tabular}{|l|l|l|l|} \hline FIGURE & NODES & REGIONS & ARCS \\ \hline 1 & 3 & 4 & 5 \\ \hline 2 & \; & \; & \; \\ \hline 3 & \; & \; & \; \\ \hline 4 & \; & \; & \; \\ \hline 5 & \; & \; & \; \\ \hline \end{tabular}

What do you notice about the information in this table?

Does you observation always work?

Can you find a network which does not fit in with your conclusions?

Would your observations still hold true if you had drawn the networks above on a ball or an inner-tube?

For homework The Bridges of Koenigsburg would just about provide the balance of activity that would expand insight into this aspect of space.