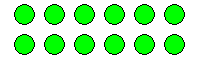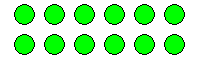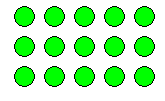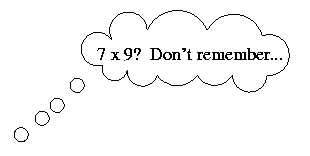Whether taught formally in school or not, the properties that
apply to numbers in operations are encountered by children during
their learning of mathematics. A sound understanding of these
properties provides a good basis for developing operations,
including mental calculation. The operation of addition comes
easily to most children, but working with multiplication requires
more sophisticated thinking and therefore usually needs more
support. Modelling number properties involving multiplication
using an array of objects not only allows children to represent
their thinking with concrete materials, but it can also assist
the children to form useful mental pictures to support memory and
reasoning.
Commutative property
The commutative property of multiplication can be neatly
illustrated using an array. For example, the array above could
be read as $2$ rows of $6$, or as $6$ columns of $2$. Or the
array could be physically turned around to show that $2$ rows
of $6$ has the same number as $6$ rows of $2$. Regardless of
the way you look at it, there remain $12$ objects. Therefore,
the array illustrates that $2 \times6 = 6 \times 2$, which is
an example of the commutative property for multiplication.
Being able to apply the commutative property means that the
number of multiplication facts that have to be memorised is
halved.
Division as the Inverse Operation of Multiplication
Of
the four operations, division is the most troublesome for young
students. Full understanding of division tends to lag well behind
the other operations. For many children opportunities to explore
the concept with concrete materials are curtailed well before
they perceive the relationships between division and the other
four operations. One such relationship, the inverse relationship
between division and multiplication, can be effectively
illustrated using arrays.
For example; 3 x 5 = 15 (3 rows of 5 make 15), can be
represented by the following array. Looking at the array
differently reveals the inverse, that is;
15 ¸3 = 5
(15 put into 3 rows makes 5 columns - or 5 in each row).
Language clearly plays an important role in being able to
express the mathematical relationships and the physical array
supports this aspect of understanding by giving the students
something concrete to talk about.
Placing the mathematics into a real-life context through word
problems can facilitate both understanding of the relationship
and its expression through words. For example, ``The gardener
planted 3 rows of 5 seeds. How many seeds did she plant?''
poses quite a different problem to ``The gardener planted 15
seeds in 3 equal rows. How many seeds in each row?'' yet both
these word problems can be modelled using the same array.
Further exploration of the array reveals two more ways of
expressing inverse relationships: 5 x 3 = 15 and
15 ¸3 = 5
. The word problems can be adapted to describe these operations
and highlight the similarities and differences between the four
expressions modelled by the one array.
Distributive property of multiplication over
addition
This rather long title not only names one of the
basic properties that govern our number system, it also names a
personally invented mental strategy that many people regularly
use. This strategy often comes into play when we try to recall
one of the handful of multiplication facts that, for various
reasons, are difficult to remember. For example, does this kind
of thinking seem familiar?
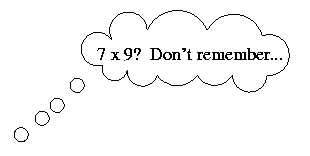
I know 7 x 7 is 49.
I need two more lots of 7, which is 14.
So if I add 49 and 14... that makes 63.
Ah yes! 7 x 9=63.''
Symbolically, this process can be represented as...
7 x 9 = 7 x (7 + 2)
= (7 x 7) + (7 x 2)
= 49 + 14
= 63.
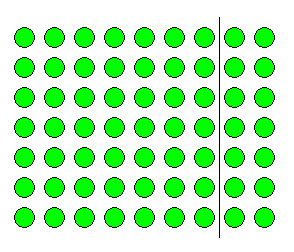
Another way to explain this process is through an array.
- The whole array represents 7 x 9 (7 rows of 9)
- The smaller array to the left of the line shows 7 x 7 (7
rows of 7).
- The small array to the right of the line shows 7 x 2 (7
rows of 2).
- It can now be easily seen that 7 x 9 is the same as (7 x 7)
+ (7 x 2), which leads to 49 + 14 = 63.
A slightly different approach to looking at this partitioned
array fully illustrates the distributive property by
highlighting the first step of splitting the 9 into 7 + 2,
before the multiplying begins. With the partition line in
place, each individual row of the whole array represents 9 = 7
+ 2. Therefore, all 7 rows represent 7 x (7 + 2), and as can be
seen on the array, this is the same as (7 x 7) + (7 x 2).