There were a number of partial solutions but
this well explained one is almost entirely the work ofAndrei of
Tudor Vianu National College and shows how "obvious" the answer
is with a little visualising and careful reasoning.
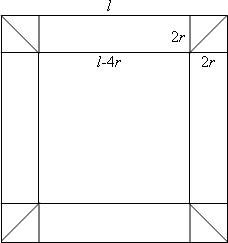
Let
be the exterior length of the cylinders and
- the radius of the
cylinders.
In the first solution, I have 4 cylinders (the 4 squares length
and
) and 8 half-cylinders - cylinders cut through the diagonal (the 8 small
right-angled triangles from the figure).
Each of the four cylinders has the volume:
Each of the half-cylinders has a volume of half a cylinder:
Now, the total volume of the tubular stand is:
With the second method, I arrange the 8 half-cylinders to make 4 bigger
cylinders, and these 4 to the bigger ones. The height of one 'big' cylinder is
, and the total volume is:
which is exactly the result obtained above.
Substituting the numerical values:
and
, I obtain:
If the volume wood would be double
, then the outside dimension
of the dowel would be:
|
|
If the volume of wood would be the same but the radius would be 1 cm,
then the outside dimension would be:
|
|
The general formula for the volume of the dowel (proved above) is:
One could see that the volume is proportional to the square of the radius,
and in the limit of long outside dimensions, proportional to the outside dimension.
