Correct solutions were received from Roy of Allerton High School, Hannah of St Helen's and St Katharines and Andre of Tudor Vianu National College, Bucharest. All used the method below. Well done to you all.

The areas are equal.

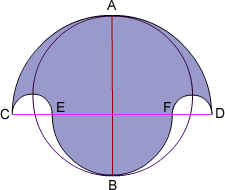
labelled diagram of salinon

The salinon is composed of semicircles on CD, EF, CE and FD.

Now we can find the area of the salinon in terms of these semicircles as follows;

Let the big semicircle on CD have a radius of $a$ , the medium one on EF be radius $b$ . Then the small circles on CE and FD have a radius of $\frac{a - b}{2}$ and the circle on AB has radius $\frac{a + b}{2}$

The area of the semicircle on CD is $π \times \frac{a^{2}}{2}$

The bottom semi circle (on EF) has an area of $π \times \frac{b^{2}}{2}$

The two smaller semi circles, on CE and FD together make a circle whose area is $π \times (\frac{a - b}{2})^{2}$

the total area of the salinon is:

the top semi circle + the bottom semi circle - the two smaller identical semi circles

or $π \frac{a^{2}}{2} + π \frac{b^{2}}{2} - π (\frac{a - b}{2})^{2}$

multiplying out all the brackets you get $\frac{π}{4} \times (a^{2} + b^{2} + 2 ab)$

now for the area of the main circle with diameter AB:

the radius of the circle is $\frac{a + b}{2}$

so the area of it is $\frac{π}{4} \times (\frac{a + b}{2})^{2}$

which, when multiplied out is the same as the area of the salinon.