There were a number of excellent
solutions to this problem which revealed three basically
different approaches that I think are all worth sharing. James
of Audenshaw School offered the following solution and
commentary, which reflects the largest proportion of your
answers. I like it very much because he explains his journey
very well.
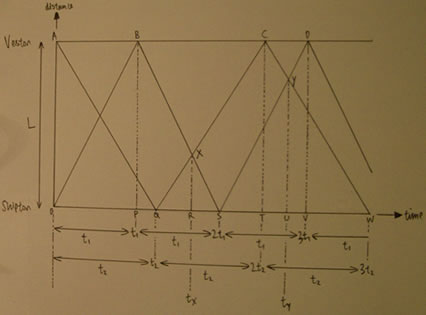
Derek adopted an approach based on a graphical
solution and using similar triangles. I have included his graph,
for interest, below. I used a graphical approach to solve this
problem the first time I met it - and I felt that my solution was
quite a neat one.
The last solution, and easily the most
elegant, was presented by Ian and Charlie of the William Lovell
School. I have added a little to their solution for clarity but
it is simple and uses no algebra - quite a surprise and very,
very nice as it makes excellent use of proportionality.
What a
lovely puzzle.
We can establish from this a couple of inequalities and I was
tempted to try this but decided it would be a pointless waste of
time though linear programming can be fun.

We can establish from this a couple of inequalities and I was
tempted to try this but decided it would be a pointless waste of
time though linear programming can be fun.
Once I had realised that x was not in fact 0 the problem becomes fairly
obvious. A bus leaving x must travel to x+y and back to 145 and the bus
leaving x+y must travel to x and then to 145. Therefore the distances
for the respective buses are:
At this point it is not known which of these journeys is the longer
journey. One may expect this to be important as it is the longer
journey that has been under taken by the faster bus. However
I can assure you that this is actually irrelevant but I will assume
Bus 2 to be the faster bus.
This gives the following equation:
This equation on its own is of course unsolvable, however if the
same technique is applied to the 3rd meeting time an equation
in terms of x and y will be achieved again. However although
it is not relevant which bus was chosen as the faster it is
very important that you select the same bus both times.
|
Bus 1: x ® x+y ® 145 ® x ® 201 |
| | |
Bus 2: x+y ® x ® 145 ® x+y ® 201 |
| |
|
Again we will assume that Bus 2 is the faster bus.
This will give the following equation
We now have two linear equations in terms of x and y which
we need to solve:
and
Solving these two equations we get
The negative sign for y has happened because
James assumed the second bus was the fastest when it was actually
the first bus.
Now all that remains is to identify which town is x and which
is x + y.
For reasons I have already explained Bus 1 was the faster bus
and we are told in the problem definition that this bus left
from Shipton and hence the slower from Veston.
In this solution Bus 1 left from x. Therefore x is Shipton
and x + y is Veston. So the milestone at Shipton is 103 miles
and the one at Veston 229 miles.
Here is the diagram
Derek used for his solution. Although his final answer was
wrong, the use of similar triangles can result in a reasonably
elegant solution.
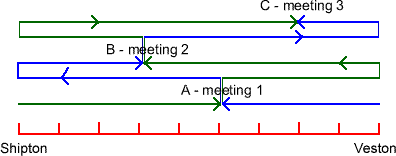
Finally Ian's and Charlie's solution, I have included a
diagram of the buses' journeys and made some minor
modifications to the text.
The fastest bus left from Shipton (green lines) and the
slower from Veston (blue lines). The diagram shows the three
meeting points for the buses as they travel between the two
towns.
The bus from Shipton travels 5 units in the same time as the bus
from Veston travels 4 units.
So first, divide the distance between the two towns into nine
equal parts.
The first meeting place is A, the second meeting place is B, and
the third meeting place is C.
The distance between B and C is : 201 - 145 = 56
56 is four units and so each unit is 14 miles.
So, to find the milestone of Veston: 201 + 28 = 229
Milestone of Shipton: 145 - 42 = 103