A graph is a mathematical object made up of points (sometimes
called nodes, see below) with lines joining some or all of the
points. You can think of the world wide web as a graph. The
points and lines are called vertices and edges just like the
vertices and edges of polyhedra. Here is a graph representing a
cube.
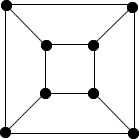
Graph Theory is a whole mathematical subject in its own right,
many books and papers are written on it and it is still an active
research area with new discoveries still being made. Graphs are
very useful in designing, representing and planning the use of
networks (for example airline routes, electricity and water
supply networks, delivery routes for goods, postal services etc.)
Graphs are also used to solve problems in coding,
telecommunications and parallel programming.
In some of these applications the actual distances and the
geometrical shape of the graph is not important, simply which
vertices in the system are linked, and these applications come
into the branch of maths known as topology. In other applications
distances between the vertices, the direction of flow and the
capacity of the 'pipes' are significant. Rather confusingly there
are two different languages used by mathematicians. You can see
some of the equivalent terminology in the table below and you
will find more at http://thesaurus.maths.org. In this article we
use the graph theory language.
|
Graph Theory
Graph
Vertex
Edge
Degree
Path
|
Network Applications
Network
Node
Arc
Order
Route
|
You can trace a path in the graph by taking a pencil, starting
at one of the vertices and drawing some of the edges of the
graph without lifting your pencil off the paper. A path is
simply a sequence of vertices where each vertex is connected by
a line to the next one in the sequence. A circuit is any path
in the graph which begins and ends at the same vertex.
Two special types of circuits are Eulerian circuits, named
after Leonard Euler (1707 to 1783), and Hamiltonian circuits
named after (William Rowan Hamilton (1805 to 1865). The whole
subject of graph theory started with Euler and the famous
Konisberg Bridge Problem.
An Eulerian circuit passes along each edge once and only once,
and a Hamiltonian circuit visits each vertex once and only
once. Both are useful in applications; the Hamiltonian circuits
when it is required to visit each vertex (say every customer,
every supply depot or every town) and the Eulerian circuits
when it is required to travel along all the connecting edges
(say all the streets in a town to collect the garbage). Note
that for a Hamiltonian circuit it is not necessary to travel
along each edge.
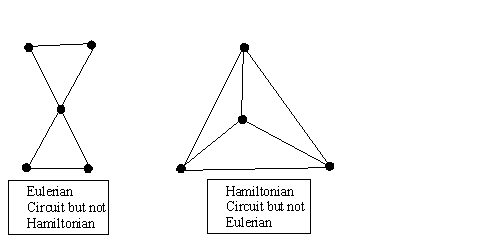
Here are two graphs, the first contains an Eulerian circuit but
no Hamiltonian circuits and the second contains a Hamiltonian
circuit but no Eulerian circuits. If you find it difficult to
remember which is which just think E for edge and E for Euler.
Can you draw for yourself other simple graphs which have one
sort of circuit in them and not the other?
Conditions for there to be Eulerian circuits are well know but
in general it is a difficult problem to decide when a given
graph has a Hamiltonian circuit. Finding conditions for the
existence of Hamiltonian circuits is an unsolved problem.
The degree of a vertex is the number of edges joining onto that
vertex, and vertices are said to be odd or even according to
whether the degree is odd or even. Euler circuits exist only in
networks where there are no odd vertices, that is where all the
vertices have an even number of edges ending there.
Two edges are used each time the path visits and leaves a
vertex because the circuit must use each edge only once. It
follows that if the graph has an odd vertex then that vertex
must be the start or end of the path and, as a circuit starts
and ends at the same vertex, for a circuit to exist all the
vertices must be even. When there are two odd vertices a walk
can take place that traverses each edge exactly once but this
will not be a circuit.
Can you think why it is impossible to draw any graph with an
odd number of odd vertices (e.g. one odd vertex)? Well the
reason is that each edge has two ends so the total number of
endings is even, so the sum of the degrees of all the vertices
in a graph must be even, so there cannot be an odd number of
odd vertices.
Here is a simple puzzle, which we call the Prime Puzzle, for
you to solve that uses and illustrates Hamiltonian circuits.
Each of the following numbers is the product of exactly three
prime factors and you have to arrange them in a sequence so
that any two successive numbers in the sequence have exactly
one common factor. The numbers are $222$, $255$, $385$, $874$,
$2821$, $4199$, $11803$ and $20677$ and we have used only the
first twelve prime numbers. First factorize the numbers, next
start to draw the graph which will have $8$ vertices, one for
each number. Take one number on a vertex and draw three edges
from it and label them, one for each factor. Now attach the
appropriate numbers at the ends of these edges. Repeat the
procedure until the graph is complete. Any two vertices are
joined by an edge if and only if they have a common factor. You
should have eight vertices and twelve edges and this should
suggest a neat way to draw the graph. You may wish to re-draw
the graph so that the edges do not cross except at the eight
vertices. The graph will be one where it is easy to find a
Hamiltonian circuit and this circuit gives you the solution to
the problem.
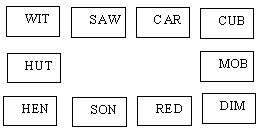
Here is a similar but well known puzzle invented by Peterson
where you have to arrange the ten cards in a loop so that each
card has exactly one letter in common with each adjacent card.
The words are HUT, WIT, SAW, CAR, CUB, MOB, DIM, RED, SON, HEN.
The arrangement shown in the diagram looks very nearly correct
but the words SON and RED do not match. If you try to solve the
puzzle by re-arranging the cards you will not succeed because
it is impossible. Now replace SON by SUN and HUT by HOT and the
puzzle can be solved. The explanation is contained in the
following two graphs.
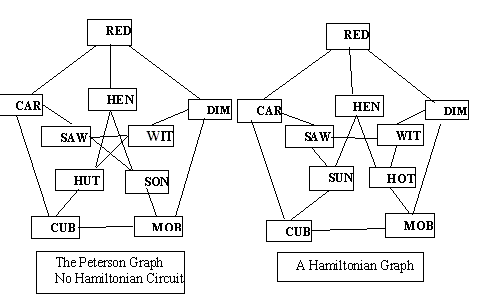 In the Peterson graph there are no Hamiltonian circuits so, unlike
the Primes Puzzle above there is no way to put the cards into the
required circuit. Changing two of the cards to SON and HUT makes
it possible to find a Hamiltonian circuit and solve the problem.
On the NRICH website you will find a lot of problems on graphs and
networks which you might like to try. Also why not do some
research on the web and find out about Euler and Hamilton, both
giants in the mathematical world.
In the Peterson graph there are no Hamiltonian circuits so, unlike
the Primes Puzzle above there is no way to put the cards into the
required circuit. Changing two of the cards to SON and HUT makes
it possible to find a Hamiltonian circuit and solve the problem.
On the NRICH website you will find a lot of problems on graphs and
networks which you might like to try. Also why not do some
research on the web and find out about Euler and Hamilton, both
giants in the mathematical world.

