This article describes what vectors are and how to add,
subtract and multiply them by scalars, and it gives some
indications of why they are useful. The article provides a
summary of the elementary ideas about vectors usually met in
school mathematics. The follow-up article 'Multiplication of
Vectors' discusses scalar products and vector products. Vectors
are an absolutely essential 'tool' in physics and a very
important part of mathematics.
There are two ways to define vectors. We can think of vectors
as points in a coordinate system corresponding to points in
space, or we can think of vectors as objects with magnitude and
direction. In this article we attempt to clarify why there are
two definitions of vectors and relate the two. The most
perceptive and mathematically able school students often feel
they don't understand the use of vectors and they are
absolutely right to question this because school textbooks
often switch between the different sorts of vectors without
justifying what they are doing.
Vectors are usually first introduced as objects having
magnitude and direction, for example translations,
displacements, velocities, forces etc. Vectors defined this way
are called free vectors
. If we simply specify magnitude and direction then
any two vectors of the
same length and parallel to each other are considered to be
identical. So by this definition a vector is an infinite set of
parallel directed line segments.
For example consider the translation three units across and one
unit up. If we apply this translation then the point $(0, 0)$
goes to $(3, 1)$, and $(5, 7)$ goes to $(8, 8)$, and every
other point is translated similarly. You can draw your own
diagrams to illustrate this. A translation of the plane moves
all the points of the plane simultaneously by the same
translation vector, so we can think of a free vector as the
same thing as a translation.
People often choose one line segment from this infinite set to
suit a particular application and it is sensible to ask why in
practice we can take a single representative without reference
to the whole set. For example, if we walk from $O$ to $A$ we
denote the displacement by $\vec{OA}$. This is different from
walking the same distance in a different direction, and
different from walking in the same direction but going a
different distance. Some people call this displacement the
vector $\vec{OA}$ but we are thinking of $O$ as a particular
point so this is one directed line segment chosen from the
whole set which constitute the free vector. If we continue our
walk from $A$ to $C$ the total displacement is the sum of these
two displacements $\vec{OA}+\vec{AC}$ and this is equal to the
directed line segment $\vec{OC}$. The triangle law is used to add free
vectors.
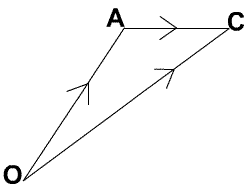
Vectors are important in navigation where the actual velocity
of an aeroplane relative to the earth is given by the combined
velocities of the wind (which carries the plane along as if it
were a glider) together with the velocity which the plane would
have in still air. In the triangle above, if $\vec{OC}$ is along
the direction required to reach the destination, and $\vec{AC}$
represents the velocity of the wind, then the pilot has to set a
course in the direction $\vec{OA}$ with a speed calculated so
that the sides of the triangle represent the velocities.
In mathematics we think of points and space as fundamental abstract
concepts and we build a model of space by using a coordinate
system. A three dimensional coordinate system is simply an
infinite set of ordered triples of real numbers $(x, y, z)$ and
each point is given by one of these ordered triples, called the
coordinates of the
point. To each free vector (or translation) there corresponds a
position vector which is
the image of the origin under that translation. So we define
position vectors as points in space and to each position vector
$P$ there corresponds a directed line segment $\vec {OP}$ which
determines an infinite set of parallel directed line segments
giving a unique free vector.
When we choose a coordinate system we effectively single out
one representative from each free vector in space, namely the one
which 'starts' from the chosen origin. If the point $A$ has
coordinates $(x_a, y_a, z_a)$ then it has position vector ${\bf
a} = (x_a, y_a, z_a)$ which may also be written as a column
vector. There is a correspondence between the point $A$, the
position vector ${\bf a}$ and the directed line segment $\vec
{OA}$ which is a representative of the infinitely many segments
making up a free vector.
It is frequently useful to work only with position vectors and
not with free vectors. While there is a conceptual distinction
between free vectors and position vectors it is possible to use
both types interchangeably but this may cause confusion if we are
not clear about the definitions.
All the vector algebra (adding, subtracting, multiplying)
which works in one system corresponds to the vector algebra in
the other system. When it suits us to do so we can switch from
free vectors to position vectors or vice versa, do the vector
algebra, then switch back with 'the answer'.
The magnitude of the
position vector ${\bf a}=(x_a, y_a, z_a)$ is defined to be
$$|{\bf a}|= (x_a^2+y_a^2+z_a^2)^{1/2}$$ and this is the length
of the line segment $\vec{OA}$ and hence it is also the magnitude
of the corresponding free vector.
The vectors ${\bf i}= (1, 0, 0), {\bf j}=(0, 1, 0)$ and ${\bf
k}=(0, 0, 1)$ are vectors of unit length parallel to the $x, y$
and $z$ axes. The position vector or point $A$ and the
corresponding free vector consisting of all directed line
segments parallel to $\vec {OA}$ can also be written as $x_a{\bf
i}+y_a{\bf j}+z_a{\bf k}$.
Some elementary textbooks say that forces are vectors but are
they? Strictly speaking they are a special type of vector with
more structure than other vectors; as well as magnitude and
direction forces are specified by their point or line of action.
If I push your right shoulder hard enough you will turn one way
and if I push your left shoulder with a force of the same
magnitude in the same direction (an equal vector) you will turn
the other way. The two forces have different turning effects so
they are different forces even though they have the same 'vector
properties'. When we add forces we simply use their vector
properties but to specify a force we need to give its magnitude,
direction and line of
action.
Addition and subtraction of vectors
To add position vectors we simply add the components. For
example if $\bf a$ is the position vector $(x_a, y_a, z_a)$ and
$\bf b$ is the position vector $(x_b, y_b, z_b)$ then ${\bf a} +
{\bf b} = (x_a+x_b,\ y_a+y_b,\ z_a+z_b).$ The {\it parallelogram
law} is used to add position vectors giving ${\vec {OA}} + {\vec
{OB}}= {\vec {OC}}$.
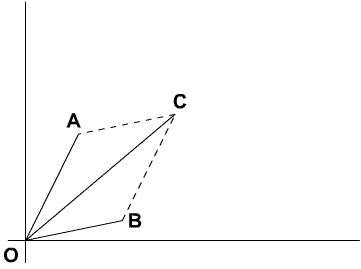
Note that, as a free vector
so the
parallelogram law of addition of position vectors exactly
corresponds to the triangle law,
, of addition of free vectors and hence they can be used
interchangeably for either type of vector.
What about subtraction? Each point A in space is a vector with
components the same as the coordinates of the point, say a=(xa,ya,za). The reflection of the point A in the origin
is the point A¢ with position vector - a=(-xa,-ya,-za). The effect of adding these two vectors is to
give the zero vector. To subtract the vector a from the
vector c simply add the vectors c and -a.
The directed line segments
and
are equal
in length and opposite in direction so we say
. The equivalent method of subtraction for free vectors can
be thought of as reversing the vector to be subtracted and adding
it to the first vector. If A and C are two points (xa, ya, za) and (xc, yc, zc) then the directed line segment
so again we see that to subtract
vectors we subtract the components.
|
|
®
AC
|
= |
®
OC
|
- |
®
OA
|
= |
æ
ç
ç
ç
è
|
|
|
ö
÷
÷
÷
ø
|
|
|
Multiplication of a vector by a scalar
We have already seen scalar multiples when we wrote (xa, ya, za) = xai+yaj+zak. Here the vectors i, j and k are multiplied by the scalars:
xa, ya and za.
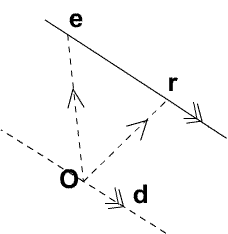
One of the uses of multiplication of vectors by scalars is to
write down an equation of a line using vectors. If a vector d is along a line then any other vector along the line is a
multiple of d and we can call d a direction
vector for the line. In writing down the equation of a line we
use the notation r = (x,y,z) for the vector of a
general point on the line, e=(x1, y1, z1) for the
vector of one particular point known to be on the line, s as a
scalar variable and d = (l,m,n) for a direction vector
along the line. The vector equation of the line is then r = e + sd.
As we have seen there are two distinct types of vectors but it is
permissable to switch from one to the other when convenient to do
so. The follow up article
'Multiplication of Vectors' completes the summary of the
basic ideas in the subject.



