Thank you to Roy Madar from Allerton High School and Andrei Lazanu
from Tudor Vianu National College, Bucharest, Romania for their
solutions.
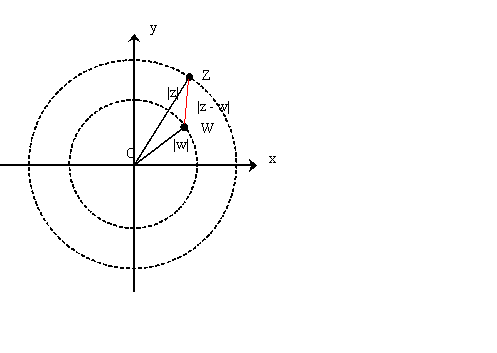
Draw two concentric circles with centres at the origin and radii
|z| and |w| and suppose, without loss of generality, that
|z| > |w| then z lies somewhere on the outer circle and w lies
somewhere on the inner circle.
In this representation, working with complex numbers is similar to
working with vectors. The two complex numbers can be added and
subtracted as vectors. So, to subtract them, it is the same as
adding one to the opposite of the other. The result is represented
in the figure. The distance between the two points representing
the complex numbers z and w is the modulus of z-w written as
|z-w|. The lengths of the sides of the triangle in the diagram
are |z|, |w| and |z-w|.
The shortest distance between any two points where one is on each
circle is given by the difference of the radii of the two circles
|z|-|w|. This would be the distance between the points z and
w if they had the same argument. If z and w have different
arguments then the distance between the points will be |z- w|
and hence |z-w| ³ |z| - |w|.
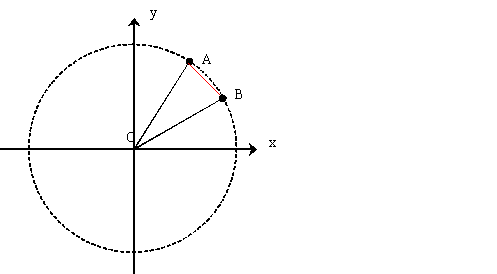
For the second part, mark points A and B on the unit circle to
represent eia* and eib* respectively where
a* and b* lie between 0 and 2p. To include all
possible values of a and b we have a = a* +2mp and b = b* + 2np for some integers m and
n. Clearly A and B also represent eia and
eib.
The chord length AB is less than or equal to the arc length
AB. Hence