Thank you Andrei Lazanu from Tudor Vianu National College, Bucharest, Romania for this solution. \par To solve the problem, I plotted three functions for $0 \leq x \leq \pi/2$. Below are the graphs of the three functions, all three plotted on the same figure with $y_1={2x\over \pi}$ in blue, $y_2 = \sin x$ in green and $y_3=x$ in red. \par 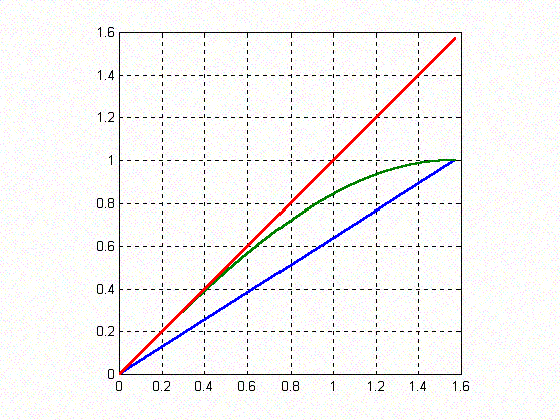graphs of sinx, x and 2x/pi

As seen from the figure, the green graph (i.e.

y = \sin x

) is situated between the other two graphs in the range of

0 \leq x \leq π / 2

. For all

x

between 0 and

π / 2

the point

(x, \sin x)

is above the point

(x, 2 x / π)

and hence

\frac{2 x}{π} \leq \sin x .

In this interval the graph of

\sin x

lies below the line

y = x

because this line meets the graph of

\sin x

at the origin and the gradient of

\sin x

is less than 1 for all

x

. Hence

\sin x \leq x

For the second part of the problem, I have to prove that:

$\frac{\tan a}{\tan b} < \frac{a}{b} .$

For any $a$ and $b$ in this interval, both $a$ , $b$ , $\tan a$ and $\tan b$ are positive, so that the original inequality is equivalent to the following one:

$\frac{\tan a}{a} < \frac{\tan b}{b}$

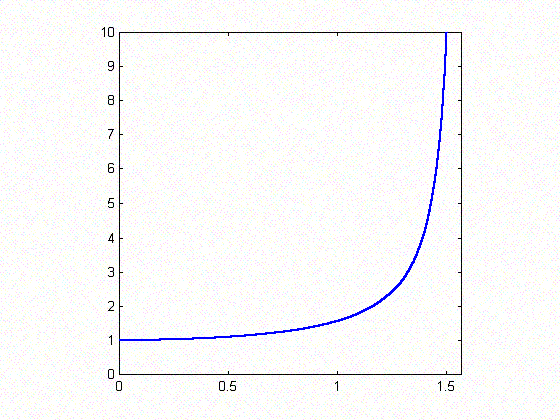
In the figure below the graph of function $y = \tan x / x$ is plotted for $0 < x < π / 2$ . y=tanx/x
I observe that the function is monotonically increasing. This means that for any $a < b$ (but remaining in the interval $0 < a < b < π / 2$ ), $y (a) < y (b)$ as required.

Alternatively, from the graph of $y = \tan x$ in this interval, if $a < b$ then the gradient of line joining the origin the point $(a, \tan a)$ is less than the gradient of the line joining the origin to the point $(b, \tan b)$ so

$\frac{\tan a}{a} < \frac{\tan b}{b}$

and hence

$\frac{\tan a}{\tan b} < \frac{a}{b} .$