Yanqing from Lipson Community College and Andrei from Tudor Vianu National College, Bucharest, Romania both sent correct solutions.

Andrei wrote: " As I am not familiar with graph theory, I first read the hint and the notes of the problem, then I looked on the web for the Maximum flow, minimum cut theorem. I found different examples, algorithms of solving such problems, as well a possible list of utilisation.

I started with the definition of terms: a cut in a network is a minimal set of edges whose removal separates the network into two components, one containing the source, and the other the sink."

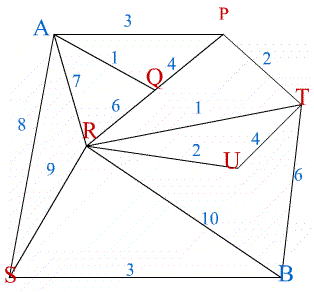
In the first network a cut through $PT$, $RT$, $RU$, $RB$, and $SB$ separates the network showing that the flow cannot be more than $18$ units (the total flow through these edges).
flow network 1
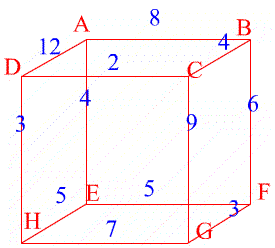
This flow is possible by sending: 3 units along ASB, 5 units along ASRB, 5 units along ARB, 2 units along ARUTB, 1 unit along AQRTB and 2 units along APTB. Hence the maximum flow is 18 units. \par In the second network a cut through BC, DC, FG and HG separates the network so the flow cannot be more than 16 units (the total flow along these edges).
flow network 2

This flow is possible by sending 3 units along ABFG, 4 units along ABCG, 2 units along ADCG, 3 units along ADHG and 4 units along AEHG. Hence the maximum flow is 16 units.