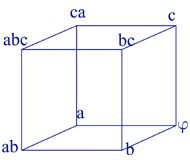
1. I observed that a cube could be represented by the diagram below, that keeps all edges and vertices (the lengths are not important).
From the beginning I observe that one could start from any vertex in a cube and there are 8 vertices.

From any vertex there are three possible routes. I shall consider the routes starting from vertex A.

Below are written all the possible combinations I found starting with the edge AD:

Path	Circuit
A-D-C-B-F-E-H-G	No
A-D-C-B-F-G-H-E-A	Yes
A-D-C-G-H-E-F-B-A	Yes
A-D-C-G-F - impossible
A-D-H-E-F-B-C-G	No
A-D-H-E-F-G-C-B-A	Yes
A-D-H-G-C-B-F-E-A	Yes
A-D-H-G-F-E - impossible

I observe that there are 6 possible paths, 4 of which are Hamiltonian Circuits.

I have to multiply the number of solutions I obtained. So the total number of solutions is given by 8 * 3 * 6 that is 144, and 96 are Hamiltonian Circuits.

Because all vertices of the cube are indistinguishable, there are 18 solutions, and 12 Hamiltonian Circuits.

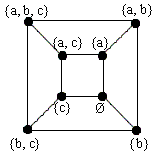
2. Set {a, b, c} has the following subsets: {a, b, c}, {a, b}, {a, c}, {b, c}, {a}, {b}, {c}, f. I observe that they could be arranged so that one subset is connected with 3 other subsets that differ from the first by only one element, deleted or inserted. These subsets can be positioned on the vertices of a cube.

I have verified that each subset is connected with 3 other subsets, forming a diagram as found before, or, more intuitively, a cube. So, the problem is reduced to the first problem. The number of sequences is 144 sequences, or 18 if the first element of the sequence does not matter.