You sent in a large number of solutions to this problem but many of them only considered the spider moving horizontally or vertically but not diagonally across the sides of the room. I have included below a net of the room with the path of the spider as it takes the shortest route over the ceiling. I hope it helps you to see what was going on. However the spider could walk around the walls to get to the fly or along the floor - risking a human foot!

spider walks over the ceiling

Andrei of Tudor Vianu National College calculated the distance the spider must travel in the original problem and has worked out when it is best to go via the floor instead of the ceiling.

 

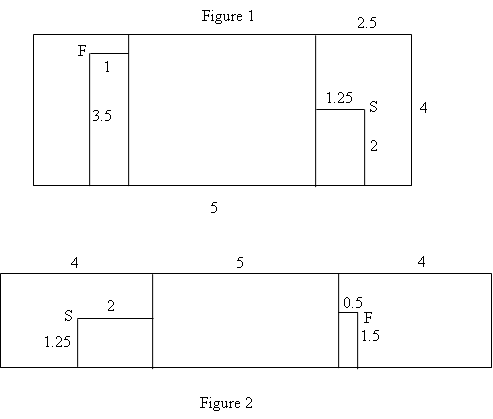
First, I observed that the shortest distance can be found on the net of the box.
In the figures below, the distances on the box are written, if the spider travels by the ceiling (figure 1) or by the lateral wall (figure 2).
diagram showing positions of spider and fly
In figure 1 - I marked the position of the fly (F), and the spider (S).
The next step is to calculate the distance travelled by the spider for each case.
Applying Pythagoras Theorem in Figure 1, I obtain:

 

FS2 = 7.252 + 1.52

FS = 7.40355 m

In Figure 2, I have:

FS2 = 7.52 + 0.252

FS = 7.50417 m

The shortest distance is 7.40355 m, i.e. the first situation. This is because the dimension "wide" is larger than the dimension "high"and the spider starts from the middle of the wall.

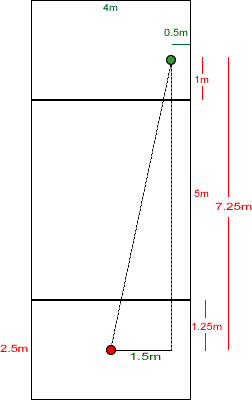
Now I analyze the situation when the fly goes down the wall. In the first case, with the fly fixed, it was situated in the upper middle of the face, so it was better for the spider to go on the top of the box. When the fly arrives at the middle (height) of the box, it is the same for the spider to go over the top or over the bottom of the box. When the fly goes still further to the bottom, the spider should go on the bottom of the box.


However in some cases it is quicker to go via the side wall instead of either the floor or the ceiling. Gillian sent us in the following diagrams to help explain how she worked out when this is the case:

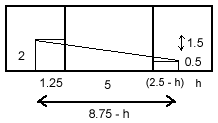
Diagram of ceiling

My first diagram shows the measurements when the spider is crawling along the ceiling. She has to go along (8.75 - h) metres and down 1.5 metres, so the shortest distance she can travel is the square root of {(8.75-h)^2 + 1.5^2}. As the height, h, of the fly decreases, the distance increases.

If she crawls along the floor, the shortest distance she can travel is the square root of {(6.25+h)^2 + 1.5^2}. As h descreases, the distance decreases. These two results could be seen just by common sense.

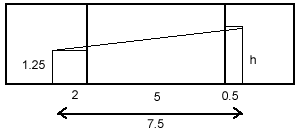
Crawling across the wall

My second diagram shows the measurements when the spider is crawling along the wall closest to the fly. This way, she goes along 7.5 metres and up (h - 1.25) metres. The shortest distance she can crawl is the square root of {(7.5^2 + (h-1.25)^2}.

At h = 1.25 metres, it is quicker for her to crawl along the wall than either the floor or the ceiling. (Distance = 7.5m, as opposed to 7.65m if she were going along the floor or ceiling.)

To see when it's quicker to go along the wall than the ceiling, I solved the inequality

(8.75 - h)2 + 1.52 ³ 7.52 + (h - 1.25)2

(8.75 - h)2 - (h - 1.25)2 ³ 7.52 - 1.52

7.5*(10 - 2h) ³ 54

h £ 1.4

When the fly is less than 1.4m from the ground, it is quicker to go by the wall than by the ceiling. Similarly, when it is higher than 1.1m, it is quicker to go by the wall than the floor.