Derek (no school given) offered the following insights into this problem: - and nicely explained too - thank you Derek.
| n-row pyramid | Ways to count 1-2-3-... |
| 1 | 1 |
| 2 | 3 |
| 3 | 7 |
| 4 | 15 |
| ... | ... |
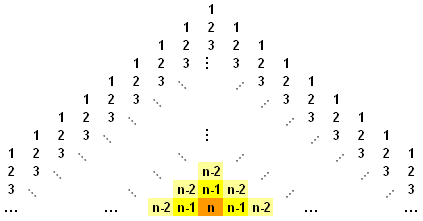

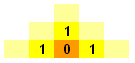
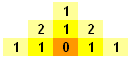
|
æ ç è |
5 k |
ö ÷ ø |
| 2 |
n-1 å k=0 |
|
æ ç è |
n-1 k |
ö ÷ ø |
Editor's comment: at this point it may be worth mentioniing that the sum of the binomial coefficients are powers of 2. Why?
Chen of the Chinese High School took a slightly different approach (similar to the one offered by Andrei of Tudor Vianu National College):
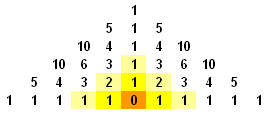
We shall define T(n) to be the number of ways to count 1 - n in a triangular array of 1 - n. We shall solve this problem by establishing a recurrence relation, and hence finding a formula for T(n). When n=1, T(1)=1 and when n=2, T(2)=3. We observe that in a triangular array of 1-3, the number of ways to get to the number '2' directly above the number '3' is given by T(2) and the number of ways to get to the '2' on the left of '3' can be easily computed to be 2. Similarly, there are 2 ways to get to the '2' on the right of the '3'. Hence, T(3)=T(2)+22=7 For T(4), we observe again that the number of ways to get to the '3' directly above of the '4' is given to be T(3). Furthermore, the number of ways to get to the '3' to the left of the '4' is the sum of the number of ways to get to the '2's adjacent to the '3'. Since by the previous result, there are 2 ways of getting to the '2', there are 2+2=4 ways of getting to the '3' to the left of the '4', and similarly for the '3' to the right of the '4'. Hence, T(4)=T(3)+2(22)=T(3)+23 Extending this argument to T(n), we obtain the recurrence T(n)=T(n-1)+2(n-1). However, since T(n-1)=T(n-2)+2(n-2), which is also equal to T(n-3)+2(n-3)+2(n-2). Thus, it is not difficult to see that T(n) = 1+2+22+23+...+2(n-1) or 2n - 1