The solution below is based on the one sent in by Barinder of Langley Grammar School. We had quite a number of correct, well laid out solutions to this problem this month including those from Roy of Allerton High School, Dan (no address given) and Calum of Wayland High School. 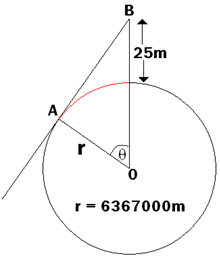cross sectional diagram of earth and lighthouse
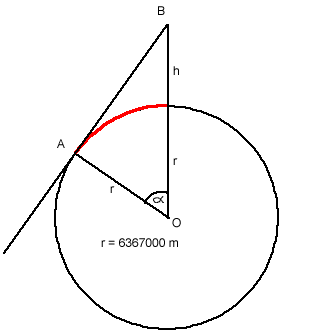
Although definitely not in proportion, this makes the problem seem a lot easier. The question is asking for the length of the arc I have coloured red. To get this, I decided to find the angle q on the diagram, and use the equation

Arc Length
= q
360
 ×2 pr

where q is measured in degrees and r is the radius ÐOAB = 90deg, since it is where a tangent and a radius of a circle meet - it is a circle theorem.

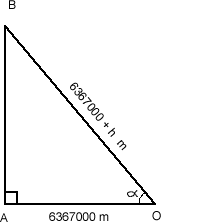
Thus, the triangle AOB can be drawn as follows:
Righta-,nagled triangle showing relevant lengths

We can now use trigonometry to find q:


cosq = 6367000
6367025

cosq = 0.99999607 q = cos-1 (0.99999607) = 0.1606 deg (4.d.p)

Substitute this into the equation for the arc length of a circle earlier to obtain the length required:

Arc Length
= 0.1606
360
 ×2pr.

Arc Length = 0.000446 ×2 ×p×6367000 = 17,842.3m = 17.8 km

For this next part, we are given the arc length, since this corresponds to the distance between England and France. The diagram is therefore:

Cross section of the Earth and the White Cliffs of dover
This is essentially the reverse of the previous question. We need to find the angle a first, and to do this, we consider the arc length of the sector OAD of the circle:

Arc Length
= a
360
 ×2 pr.


So 32,000 = a
360
 ×2 ×p×6367000.

Then 32,000 ×360 = a×2 ×p×6367000 .

So a = 0.288o(3.d.p)

Right-angled triangle showing lengths
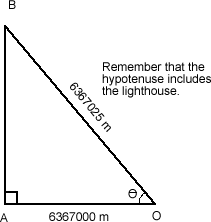
Since we now have the angle a, we can consider the triangle AOB:


cosa = 6367000
6367000 + h

.

So
6367000 + h = 6367000
cos(0.288)

.


So 6367000 + h = 6367080.415

h = 6367080.415 - 6367000 = 80.415 m high.

Thus, the cliffs of Dover are 80.4 metres high.