Thomas sent in the solution below. We also received a correct
solution from Andrei of School 205 Bucharest as well as a number
of partial solutions.
The description of the thirteen axes of revolution are as
follows:
- three of them penetrate the cube
through the centre of a given face and exit through the center
of the opposite face (using a die as an example, through the 1
and 6, 2 and 5, and 3 and
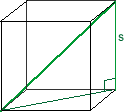
- four of them penetrate the cube
through a given vertex and exit through the opposite vertex (if
the cube were to be stood on a vertex, it would exit through
the one on top);
- the other six enter the cube
through the midpoint of a given edge and exit through the
midpoint of the opposite edge (if the cube were stood on edge,
it would exit through the midpoint of the top edge).
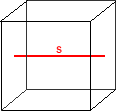
As for the mean length of the axes, the three axes through the
face have the same length as an edge (call that length
s
).
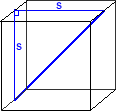
the six edge axes have a length equal to the diagonal of a
face, or
s ×Ö2
and the four vertex axes, the hypotenuses of right triangles
with sides of
s
and
s ×Ö2
, have length:
s ×Ö3
.
Summed up, the average axis length is:
.