We received correct solutions from Alice, Joanna from Woodmill High School, Derek, Robert from Ardingly College Junior School and Joe from Lady Manners School in Bakewell. Well done to you all.
Robert summarised his findings as follows:
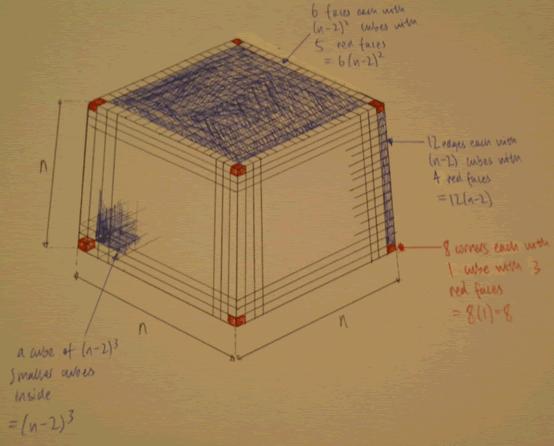
"Let n= number to be cubed
No. of small cubes with 6 red sides = (n-2) cubed
This is because the cubes in the centre remain clean, so you must take one off either edge and then cube it.
No. of small cubes with 5 red sides = 6((n-2) squared)
This is because there are 6 faces to the cube, and only the ones not on the edge remain clean on 5 sides. So you must take one off either edge, then square it, then multiply it by the 6 faces.
No. of small cubes with 4 red sides = 12(n-2)
This is because there are 12 non-corner edges which is multiplied by n (which = 1 whole edge) -2 for the 2 corners.
No. of small cubes with 3 red sides = 8
This is because there are always 8 corners
The total No. of small cubes is always n cubed"
Alice described her findings in a similar way:
"First of all I imagined a 3x3x3 cube being dipped in paint - that's how I worked the first one out then we worked out that
1) the number of cubes with 6 red faces equalled (n-2) cubed, like when you take the skin off a square orange taking a layer off each side
2) 5 red faces 6(n-2) squared, which is like the above but for the faces instead of the middle (its squared not cubed ) and you have to times it by 6 because there's 6 faces
3) 4 red faces 12(n-2) this is the edges, take 2 for the corners and times by 12 because that's how many edges there are
4) always got to be eight because these are corners, unless your cube is 1x1x1
5) total number of small cubes is n cubed"
Joe, Derek and Alice completed the table of results:
|
Size of large cube |
No. of small cubes with 6 red faces |
No. of small cubes with 5 red faces |
No. of small cubes with 4 red faces |
No. of small cubes with 3 red faces |
Total No. of small cubes |
|
3 x 3 x 3 |
1 |
6 |
12 |
8 |
27 |
|
4 x 4 x 4 |
8 |
24 |
24 |
8 |
64 |
|
5 x 5 x 5 |
27 |
54 |
36 |
8 |
125 |
|
6 x 6 x 6 |
64 |
96 |
48 |
8 |
216 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
10 x 10 x 10 |
512 |
384 |
96 |
8 |
1000 |
|
23 x 23 x 23 |
9261 |
2646 |
252 |
8 |
12167 |
|
n by n by n |
(n-2)^3 |
6(n-2)^2 |
12(n-2) |
8 |
n^3 |
NB. The values for n are correct unless n = 1.
When n = 1 the single cube will have no red faces.
In her conclusion Alice added that in the second column the numbers were all cubic numbers, in the third column square numbers times 6 and in the fourth column multiples of 12.
Derek added:
We can verify that all cubes have been accounted as:
|
|
|
|
Derek added this diagram to support his conclusions:
