We received three excellent solutions from Jonathan, Bryn and Marissa of Madras College. Marissa's solution follows:

A tilted square is a shape (all equal sides, 4 right angles) that is standing on its corner. This can be described as "so many across, so many up"

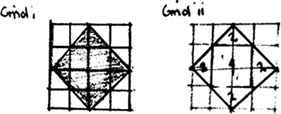
Grids 1 and 2

This is an example of a "2 along, 2 up" tilted square (Grid i).

We can find the area by drawing an upright square inside the tilted square so long as it covers full units (1 Grid ii). You then find the unit area of the 4 right angled triangles of the outside of the upright square in the inside of the tilted square (2 Grid ii).

In this investigation I am trying to show which numbers are possible and impossible for the area of a tilted square. I also hope I will be able to show you some problems in numbers as well.

1 ups
I will start with the basic "1 up" sequence. It goes as follows:

Do you now understand from the illustrations how the "1 ups" go?

I will now draw a table showing the areas, uses of triangles and squares.

along	up	area of upright square +	(number of triangles	x area of triangle)	= area of titled square
1	1	0	4	1/2	2
2	1	1	4	1	5
3	1	4	4	1 1/2	10
4	1	9	4	2	17
5	1	16	4	2 1/2	26
6	1	25	4	3	37
7	1	$x^{2} + 4$	4	n/2	a (area)

So the formula of the "1 up" titled squares is: n along 1 up -->

(n - 1)^{2} + (4 \times \frac{1}{2} n) = a

The numbers of the areas also have a pattern:

x	1	2	3	4	5	6	x
area	2	5	10	17	26	37	$x^{2} + 1$

Now let's study the...

2 ups

The "2 up" sequence is like this:

I will now make another table illustrating the "2 ups"

along	up	area of upright square +	(number of triangles	x area of triangle)	= area of tilted square
1	2	1	4	1	5
2	2	4	4	1	8
3	2	1	4	3	13
4	2	4	4	4	20
5	2	9	4	5	29
6	2	4	4	6	40
n	2	?	4	n	a (area)

n is not easy to find here because there is no regular pattern in the "area of an upright square column". I will now try and find a pattern in the numbers of areas.

x	1	2	3	4	5	6	x
area	5	8	13	20	29	40

Therefore the area of a "2 up" tilted sqaure is equal to

But wait a minute...

could the formula for "3 ups" possibly be

Could "4 ups" be

Using this formula we could also find what areas are not "2 up" tilted squares. Let's take the number 260

Now let's try 580

Let's look at the pattern for the area of "3 ups"

x	1	2	3	4	5	6	x
area	10	13	18	25	34	45

Let's see "4 ups"

x	1	2	3	4	5	6	x
area	17	20	25	34	45	58

This proves that to be an area of a titled square, the number must be the sum of two square numbers.

= area of a tilted square

If you were also only given the numer along and number up you could find the area because

number along2 + number up2 = area

This can be proved by Pythagoras' theorem.

------------------------------------------------------------------------------------------------

n across, 1 up set produces squares with areas of

n^{2} + 1

A square whose area is 122 square units has an 11 across, 1 up base

and a square whose area is 2501 square units has a 50 across, 1 up base.

n across, 2 up set produces squares with areas of

n^{2} + 4

A square whose area is 260 square units has an 16 across, 2up base

and a square whose area is 580 square units has a 24 across, 2up base.

n across, 3 up set produces squares with areas of

n^{2} + 9

n across, x up set produces squares with areas of

n^{2} + x^{2}