We had a number of partial solutions,
including some from The Mount School in York. The two correct
solutions which were sent in from David of the Wreake School
and Andrei of Tudor Vianu National College have been used as
the basis of what is below. Well done David and Andrei. It
looks as if the animation helped to see what was going on and
to develop a strategy that could then be represented in
algebraic form.
For a 4x4 array, it was possible to complete the change in 21
moves, which the animation said was the minimum.Trying for
grids from 2x2 to 5x5, the results are written in the following
table:
| Array |
Moves |
| 2x2 |
5 |
| 3x3 |
13 |
| 4x4 |
21 |
| 5x5 |
29
|
It is clear that the difference in the number of moves is
always 8.
Now, to predict the necessary number of moves.
Let's imagine the square grid of side n. As 5 is the starting
number, and 8 is taken (n-2) times, we obtain:
5 + 8(n-2) = 8n -16 + 5 = 8n- 11
That is for a grid of size n x n the number of moves seems to
be from the pattern 8n-1.
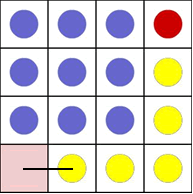
However, to prove this general formula,we need to analyse the
moves: a) the blue counters from the figure below:
The sketch is done for a 4 x 4 array, but it could be
generalised for an n x n array.
To make the first space for the red counter we need to create
a space below it. This requires you to move the counters
(coloured yellow here) along the last row and down the last
column.
In an n x n array, there are blue counters on every place of
two sides, except the ends, and one in the place of
intersection of the two sides.
So, in total there are: 2(n- 2) + 1 = 2n- 4 + 1 = 2n -3 blue
counters needing that number of moves.
b) Now the red counter can move one place down:
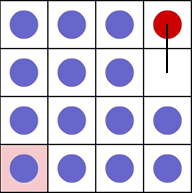
c) there is a series of repeated moves from now on:
There is a pattern which means that the red counter will move
every third go, so that the red counter travels around the
diagonal of the array.
In the figure below the path of the red counter from the last
position, to home is represented.
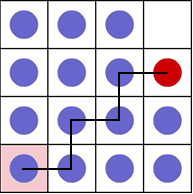
Overall, from this position, the red counter moves n - 2 squares
down and n - 1 squares across. So we have:
n - 1 + n - 2 =2n - 3
Each time the red counter moves, two blue counters have to be
moved to fill the empty space and create a new one that the red
counter can move into. So, we obtain:
3(2n- 3).
Now, adding all the results to calculate the total number of
moves:
(2n -3) + 1 + 3(2n -3) = 2n -3 + 1 + 6n -9 = 8n -11
Which matches the prediction.
Andrei also noted that the number of moves is always odd because
8n is always even and 11 is odd. For the 4x4 array, the red
counter makes its moves on moves 6, 9, 12, 15, 18 and 21.
For the rectangular case, a similar strategy can be used.
Suppose the rectangle has m rows and n columns, with m > n.
First of all, we need m + n - 3 moves to get the space to next to the red
counter. Then, we need use one move to put the red counter in thisspace.
We can then move (n-1) squares down and (n-1) across, using three moves
per squareas before.
Now we must move down the last (m-n-1) squares. This takes 5 moves for each
square, as we do not alternate between horizontal and vertical moves.
Adding all this up, the total number of moves needed is
|
n + m - 3 + 1 + 2 ×3(n-1) + 5(n-m-1) = 2n + 6m - 13. |
|