Thanks to Andrei of School 205 Bucharest for this well explained solution.

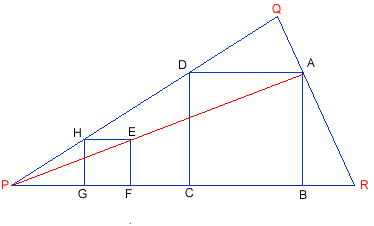
First, I drew a line HG, perpendicular on P, and a line through H, parallel with PR.

Then I finished drawing the square HEFO, drawing EF perpendicular on PR.
The line PE intersects QR in A.
From A I drew a parallel to PR (let the intersection point with PQ be D), and a perpendicular to PR (let the intersection point with PR be B).
This way I found 3 vertices of the rectangle ABCD, and I finished the rectangle finding the vertex C on PR, so that CD is perpendicular to PR.

The rectangle ABCD is a square because:- Triangles PEF and PAB are similar, they are both right-angled triangles, with a common angle. The similarity ratio is:

PE
PA
= EF
AB

(1)
Triangles PEH and PAD are similar, because angles PEH and PAD are equal and HPE is a common angle. The similarity ratio

PE
PA
= HE
AD

(2)
From (1) and (2)

AB
EF
= AD
HE

As HE=EF (sides of a square) Therefore AB = AD ABCD is a rectangle with two adjacent sides equal

Therefore ABCD is a square.

solution

Now, the construction of the inscribed square must be done in the following steps:

Chose a point H on side PQ, near P
Draw line HG, perpendicular on PR
Take the distance HG as the compass distance, and draw a circle arc, with centre G. F is the point of intersection of this arc with PR.
Construct two circle arcs with centres F and H (with the same radius as before). Their intersection is point E, and EFGH is a square.

Draw from A parallel to EF and HE. Their intersections with PR and QP are points B and D respectively.
Draw from D a parallel to AB. Its intersection with PR is C.
ABCD is the square to be found.

Note

The choice of point P, so that E is interior to the triangle PQR is not a restrictive condition, the construction is the same if E is exterior to triangle PQR.