Congratulations Andrei Lazanu, age 14, of School No. 205,
Bucharest, Romania for this excellent solution.
I looked at the images of points (1, 0) and (0, 1) respectively,
under the transformation by the matrix $$ \left(
\begin{array}{cc} a & b \\ c & c \end{array} \right) $$
$$ \left( \begin{array}{cc} a & b \\ c & d \end{array}
\right) \left( \begin{array}{c} 1 \\ 0 \end{array} \right) =
\left( \begin{array}{c} a \\ c \end{array} \right) $$
This means that under this transformation, the point (1, 0) maps
to the point $(a,c)$. $$ \left( \begin{array}{cc} a & b \\ c
& d \end{array} \right) \left( \begin{array}{c} 0 \\ 1
\end{array} \right) = \left( \begin{array}{c} b \\ d \end{array}
\right) $$ Under this transformation, the point (0,1) maps to the
point $(b,d)$.
Now, I look at the effect on the plane of the four
transformations:
1. $b = c = 0,\ a = d =
-1$ $$ \left( \begin{array}{cc} -1 & 0 \\ 0 & -1
\end{array} \right) \left( \begin{array}{c} x \\ y \end{array}
\right) = \left( \begin{array}{c} -x \\ -y \end{array} \right)
.$$ This means each point (x, y) transforms into its symmetrical
image with respect to the origin, i.e. into the point (-x, -y).
This is a rotation of 180 degrees about the origin.
2. $b = c = 0,\ a = - 1,\
d = 1$ $$ \left( \begin{array}{cc} -1 & 0 \\ 0 & 1
\end{array} \right) \left( \begin{array}{c} x \\ y \end{array}
\right) = \left( \begin{array}{c} -x \\ y \end{array} \right) .$$
Here, it is a reflection in the y-axis.
3. $b = c = 0,\ a = d =
1$ $$ \left( \begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}
\right) \left( \begin{array}{c} x \\ y \end{array} \right) =
\left( \begin{array}{c} x \\ y \end{array} \right) .$$ In this
situation each point transforms into itself.
4. $b = c = 0,\ a = 1,\ d
= -1$ $$ \left( \begin{array}{cc} 1 & 0 \\ 0 & -1
\end{array} \right) \left( \begin{array}{c} x \\ y \end{array}
\right) = \left( \begin{array}{c} x \\ -y \end{array} \right) .$$
This transformation leaves the abscissa unchanged and modifies
the sign of the ordinate, being a reflection in the x-axis.
Now, I look at the next set of transformations.
5. $a = d = 0,\ b = c =
1$ $$ \left( \begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array}
\right) \left( \begin{array}{c} x \\ y \end{array} \right) =
\left( \begin{array}{c} y \\ x \end{array} \right) .$$ In this
transformation, the abscissa and the ordinate are interchanged,
the transformation being a reflection in respect to the line
$y=x$, the angle bisector of the first quadrant.
6. $a = d = 0,\ b = 1,\ c
= -1$ $$ \left( \begin{array}{cc} 0 & 1 \\ -1 & 0
\end{array} \right) \left( \begin{array}{c} x \\ y \end{array}
\right) = \left( \begin{array}{c} y \\ -x \end{array} \right) .$$
Looking to the solution to 'Complex Rotations' from the NRICH
+15, July 2003, I see that this comes to the transformation of
point C into point G: here the plane is complex, on the abscissa
there is the real part, and the ordinate the imaginary one, but
in fact the things are completely similar. This is a rotation of
270 degrees anti-clockwise about the origin.
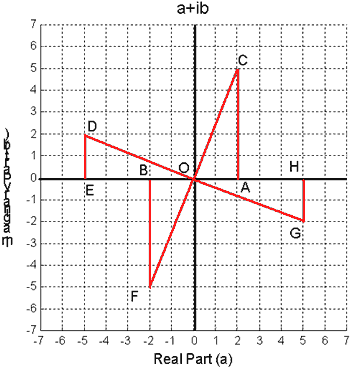
The lines CF and DG are perpendicular. All four triangles are
congruent, because they are all right-angled triangles and all
have two congruent sides.
7. $a = d = 0,\ b = c =
-1$ $$ \left( \begin{array}{cc} 0 & -1 \\ -1 & 0
\end{array} \right) \left( \begin{array}{c} x \\ y \end{array}
\right) = \left( \begin{array}{c} -y \\ -x \end{array} \right)
.$$ This corresponds to a reflection in the line $y=-x$.
8. $a = d = 0,\ b = -1,\
c = 1$ $$ \left( \begin{array}{cc} 0 & -1 \\ 1 & 0
\end{array} \right) \left( \begin{array}{c} x \\ y \end{array}
\right) = \left( \begin{array}{c} -y \\ x \end{array} \right) .$$
This corresponds to a rotation of the point by 90 degrees
anti-clockwise about the origin.
The difference between the transformations (5 - 8) and the
transformations (1 - 4) is that not only the signs are changed,
but a reversal of the x and y coordinates takes place
simultaneously.
I start to analyse the effect of these transformations on the
unit square with vertices (0,0), (0,1), (1,1), (1,0). By
observing what happens to the two points A(1,0) and B(0,1) we can
see what happens to the whole square which moves rigidly with the
edges OA and OB. All the points in the plane are transformed in
the same way as the unit square.
1) The matrix $$ \left(
\begin{array}{cc} -1 & 0 \\ 0 & -1 \end{array} \right) $$
maps (1,0) to (-1,0) and (0,1) to (0,-1), a rotation of 180
degrees about the origin.
2) The matrix $$ \left(
\begin{array}{cc} -1 & 0 \\ 0 & 1 \end{array} \right) $$
maps (1,0) to (-1,0) and (0,1) to (0,1), a reflection in the
y-axis.
3) The matrix $$ \left(
\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array} \right) $$
maps (1,0) to (1,0) and (0,1) to (0,1), the identity
transformation which leaves all points unchanged.
4) The matrix $$ \left(
\begin{array}{cc} 1 & 0 \\ 0 & -1 \end{array} \right) $$
maps (1,0) to (1,0) and (0,1) to (0,-1), a reflection in the
x-axis.
5) The matrix $$ \left(
\begin{array}{cc} 0 & 1 \\ 1 & 0 \end{array} \right) $$
maps (1,0) to (0,1) and (0,1) to (1,0), a reflection in the line
$y=x$.
6) The matrix $$ \left(
\begin{array}{cc} 0 & 1 \\ -1 & 0 \end{array} \right) $$
maps (1,0) to (0-1) and (0,1) to (1,0), a rotation of 90 degrees
clockwise or 270 degrees anti-clockwise about the origin.
7) The matrix $$ \left(
\begin{array}{cc} 0 & -1 \\ -1 & 0 \end{array} \right) $$
maps (1,0) to (0,-1) and (0,1) to (-1,0), a reflection in the
line $y=-x$.
8) The matrix $$ \left(
\begin{array}{cc} 0 & -1 \\ 1 & 0 \end{array} \right) $$
maps (1,0) to (0,1) and (0,1) to -1,0), a rotation of 90 degrees
anti-clockwise about the origin.
