
$$\frac{n(n+1)}{2}$$ $$\frac{(n-1)(n+1)}{4} +1$$ $$(\frac{n+1}{2})^2$$ $$(\frac{n+1}{2})^2$$ $$ (n+1)(n+3)\over 8$$
original text of problem
A square tablecloth is coloured in. Colour the squares so that each square is the same colour as all the symmetrically placed squares and a different colour from the rest of the squares.
This means that the tablecloth will look the same if it is turned around or turned over.
How many colours do you need for table cloths of side $3 \times3$, $5 \times5$, $7 \times7$, $9 \times9$ squares.
Prove that for an $n \times n$ tablecloth (where $n$ is odd) the number of colours needed is
$$(n+1)(n+3)\over 8$$
*Original version of interactivity:
Original solution
A starting point was sent in by a group of anonymous students looking at the first four tablecloths with sides of odd length.

We placed the same colour in each of the corners, then worked around the cloth using different colour but keeping in symmetry.
Anthony and Samantha of Bentley Park College Australia offered the following:
We only found patterns here but we couldn't work out a way to prove that for an $n \times n$ tablecloth (where $n$ is odd) the number of colours needed are:
$(n+1) \times (n+3)$ divide by 8, although it did work we can't prove it.
| Squares | Patterns |
| $3 \times 3=3$ | $3+3 =6$ |
| $5 \times 5=6$ | $6+4 =10$ |
| $7 \times 7=10$ | $10+5 =15$ |
| $9 \times 9=15$ | $15+6 =21$ |
| $11 \times 11=21$ | etc |
Squares
The pattern here was that the amount of squares in each one subtracted with the next answer would create a pattern of $3$,$4$,$5$,$6$ etc.
These are the triangular numbers. Can you see why?
Charlene from Brunei sent us the following solution which shows nicely how the problem can be broken down. Many thanks for this Charlene.
We'll have a look at the $7\times 7$ square.
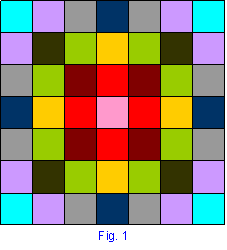
Notice that Fig.1 can be 'stripped' off layer by layer to get the following so that when fitted inside each other they turn out to make Fig. 1
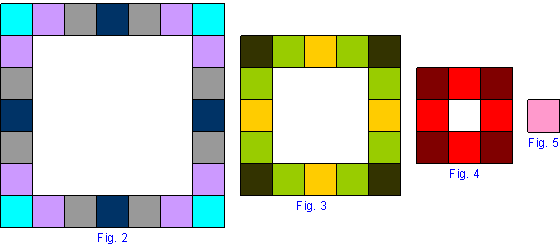
Notice that Fig.5 has one colour, Fig. 4 has two colours, Fig.3 has three colours and Fig. 2 has four colours.
It can be seen that the number of different colours for shells (not the whole square!) with side length $n$ is equivalent to
$(n + 1)/2$
Of course, this only applies to odd values of $n$.
Now, all we have to do to find the number of different colours in the square is to work out the following sum
$1 + 2 + 3 +? + (N + 1)/2$ where $N$ is the value of the outermost shell of the square.
By using the Gauss pairing tool we get
$(N + 1)/2 \times[(N + 1)/2 + 1] \times1/2 = [(N + 1) \times(N + 3)]/8$
as required.
Correct solutions were also received from Tyrone, Alex and Andrei. Well done to you all .