Many people worked well on this problem. Some of the best efforts came from, Rebecca Pocock, Rebecca Greenhalgh, Chung Leung, Jasmine Humphries, Liana and Stephie (Age 10, Crofton Junior School, Kent), Jessica Cattermole (Age 10), Jaimee Micelli (Age 11) and Christopher Block (Age 10, Tattingstone School, UK). These people did well because they tried to find lots of Abundant Numbers and showed all the factors they'd used. Rachel Corner (Age 10, Crofton Junior School, Kent) did a particularly good job of testing the first 80 counting numbers.
Here is a list of abundant numbers. I'm sure there are many more!
| Abundant Number | Factors | Total |
|---|---|---|
| 12 | 1, 2, 3, 4, 6 | 16 |
| 18 | 1, 2, 3, 6, 9 | 21 |
| 20 | 1, 2, 4, 5, 10 | 22 |
| 24 | 1, 2, 3, 4, 6, 8, 12 | 36 |
| 30 | 1, 2, 3, 5, 6, 10, 15 | 42 |
| 36 | 1, 2, 3, 4, 6, 12, 18 | 55 |
| 40 | 1, 2, 4, 5, 8, 10, 20 | 50 |
| 42 | 1, 2, 3, 6, 7, 14, 21 | 53 |
| 48 | 1, 2, 3, 4, 6, 8, 12, 16, 24 | 76 |
| 54 | 1, 2, 3, 6, 9, 18, 27 | 66 |
| 56 | 1, 2, 4, 7, 8, 14, 28 | 64 |
| 60 | 1, 2, 3, 4, 5, 6, 10, 12, 15, 20, 30 | 108 |
| 70 | 1, 2, 5, 7, 10, 14, 35 | 74 |
| 72 | 1, 2, 3, 4, 6, 8, 9, 12, 18, 32, 35, 64 | 194 |
| 78 | 1,2, 3, 37, 39 | 82 |
| 80 | 1, 2, 4, 5, 8, 10, 16, 20, 40 | 106 |
| 84 | 1, 2, 3, 4, 6, 7, 12, 14, 21, 28, 42 | 140 |
| 90 | 1, 2, 3, 5, 6, 9, 10, 15, 30, 45 | 126 |
| 100 | 1, 2, 4, 5, 8, 10, 20, 25, 50 | 125 |
Rowena Scott noticed that the example given (48) had a lot of factors, and so used this idea to choose some numbers that she knew had lots of factors to test (12 and 24).
Daniel Loh (Age 10, Anglo-Chinese School, Singapore) noticed something else about Abundant numbers. Does this always work? Why or why not?
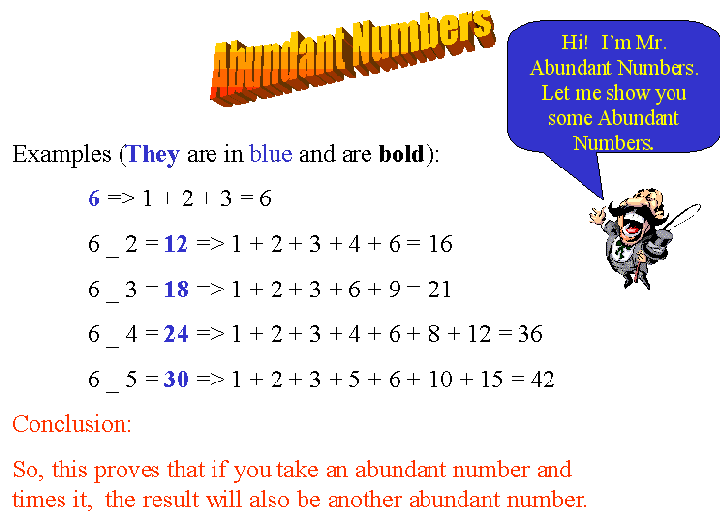
Chung Leung (Age 10, Crofton Junior School, Kent) found enough factors of one million to be sure is was an abundant number!