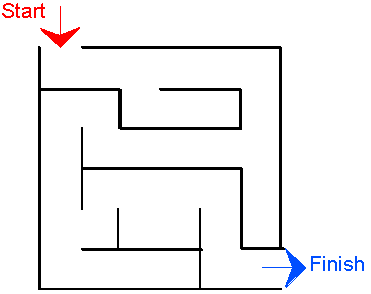
Here is a very simple maze:

It was made on square 'dotty paper'.

First you choose a size - this maze was 6 x 6, but you can use a larger size such as 10 x 10.

Draw out the outside box leaving spaces for the start and finish. These can be wherever you like.

Next draw the path, with plenty of false trails, going through every square. The pictures show how the maze was constructed.

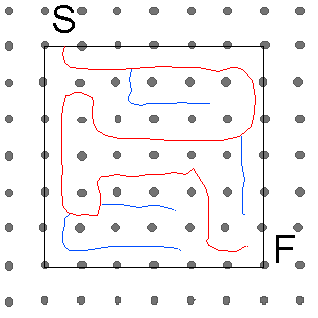
Remember to draw the path very faintly so it can be rubbed out at the end.

Next the 'walls' are put in wherever the paths do not go into the next square.

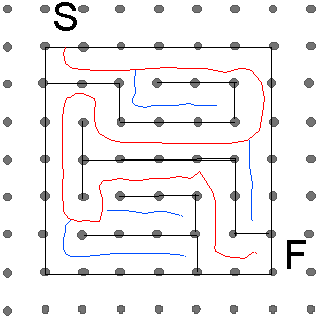
Finally the outer square is redrawn leaving gaps for the start and exit and the paths, both true and false, are rubbed out.

Much more intricate mazes can be made this way by making the original square 10 x 10 or even larger. Remember that the paths must go into each square on the dotty paper once and once only because otherwise you might make a short cut. Two paths must never cross. The finished maze should have only one solution.

What does make a maze harder to do?

Does where the start and finish are in relation to each other make a difference?

Do the number of false trails make it more complicated or is it only a question of size?

Make several mazes of the same size (you could do this with a group of maze- makers) and see which are the most difficult to do.

Perhaps you could make a circular maze in a similar way by first drawing a set of concentric circles with lines radiating through them.

Or you could try to make a maze with triangular or hexagonal cells or with curved lines.

Which of these do you think would make the maze most difficult to follow?

A maze like this can be made much larger, with many more false trails, and so much harder. Of course you could use many other shapes besides hexagons to make it from.

Here is another different sort of maze. It is the same 6 x 6 size as the one we started with but has fewer walls. There are numbers in each of the cells. You go through adding all the numbers that you pass. You may not go through any cell more than once.

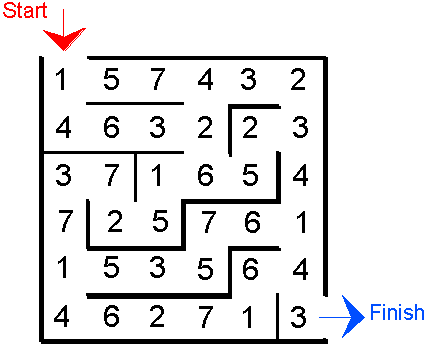
Can you find a way through in which the numbers add to exactly 100?

Can you make up an even harder maze than this with numbers in it?