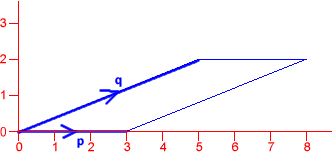
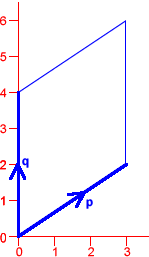
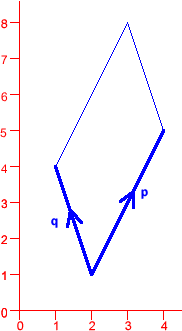
Here are two parallelograms, defined by the vectors
$\mathbf{p}$ and $\mathbf{q}$. Can you find their areas?
$$\mathbf{p}=\left(\begin{array}{c}3\\ 0\end{array}\right),
\mathbf{q}=\left(\begin{array}{c}5 \\ 2\end{array}\right)$$
$$\mathbf{p}=\left(\begin{array}{c}3 \\ 2\end{array}\right),
\mathbf{q}=\left(\begin{array}{c}0 \\ 4\end{array}\right)$$
Select different vectors $\mathbf{p}$ and $\mathbf{q}$ and find
the areas of the corresponding parallelograms. Can you discover a
quick way of doing this?
Here are two more parallelograms, again defined by vectors
$\mathbf{p}$ and $\mathbf{q}$. This time, neither $\mathbf{p}$
nor $\mathbf{q}$ lies along an axis. Can you find the areas of
these parallelograms?
$$\mathbf{p}=\left(\begin{array}{c}4 \\ 1\end{array}\right),
\mathbf{q}=\left(\begin{array}{c}3 \\ 3\end{array}\right)$$
$$\mathbf{p}=\left(\begin{array}{c}2 \\ 4\end{array}\right),
\mathbf{q}=\left(\begin{array}{c}-1 \\
3\end{array}\right)$$
Try some others.
Now try to generalise this. Can you find the area of the parallelogram
defined by the vectors
and
?