This problem is about investigating whether it is possible to start at one vertex of a platonic solid and visit every other vertex once only- returning to the vertex you started at.

This is quite difficult to visualise in 3D so this problem involves drawing 2D skeletons of the five Platonic solids (known as Schlegel graphs) and using these to try to answer the challenge we have set you below.

Schlegel graphs are very useful in studying molecular structure. It is as if all the edges were made of elastic and they have been stretched out to make the skeleton flat. Here is a cube and its Schlegel graph:

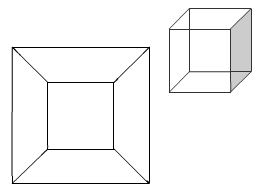
Can you sketch the skeletons on paper for the tetrahedron, octahedron, dodecahedron and icosahedron? When you think you have a skeleton - you can check your own answer by clicking to reveal the Schlegel graphs.

   

  
 

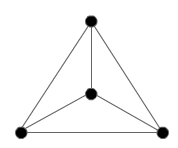
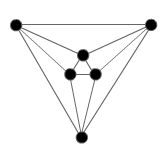
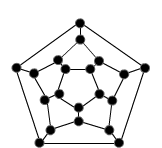
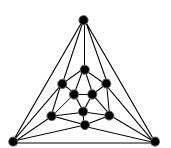
The problem is in two parts:

· to find the paths along the edges of the solids that enable you to visit every vertex and
· to describe the strategies you have used and what you discovered. For example: is the path unique?

These paths are called Hamiltonian Circuits after the Irish mathematician William Hamilton who also invented this game in 1857.