Copyright © University of Cambridge. All rights reserved.
'Crescents and Triangles' printed from https://nrich.maths.org/
Show menu
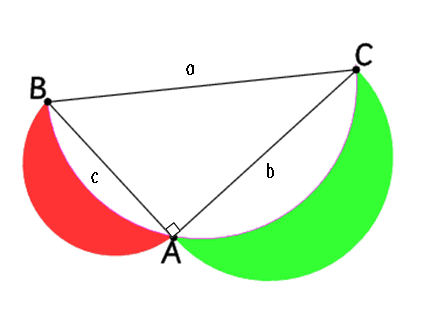
The trick with this question was not to make life difficult by working values out. As a consequence some of you managed much more elegant solutions than others. Here is an example based on that offered by Shu Cao (very well done). Jeongmin Lee, Rebecca Bartram (The Mount School, York) and Andrei Lazanu (School 205, Bucharest) should also be congratulated.
Using Pythagoras` theorem in
$ABC$,
$$\begin{eqnarray}a &=& \sqrt{b^2 + c^2} \\ \mbox{Area
of semicircle on BC} &=& \pi \frac {a^2}{4}\\ &=&
S1\\ \mbox{Area of semicircle on AC} &=& \pi \frac
{b^2}{4}\\ &=& S2 \\ \mbox{Area of semicircle on AB}
&=& \pi \frac{c^2}{4}\\ &=& S3\\ \mbox{Area of
crescents} &=& S2 + S3 + \mbox{Area ABC} - S1\\ &=&
\pi \frac {b^2}{4} +\pi \frac {c^2}{4} + \mbox{Area ABC} - \pi
\frac {a^2}{4}\\ &=& \pi \frac {b^2}{4} + \pi \frac{c^2}{4}
- \pi \frac {a^2}{4} + \mbox{Area ABC}\\ &=& \frac{\pi}{4}
\times ( b^2 + c^2 - a^2 ) + \mbox{Area ABC}\\ &=& 0 +
\mbox{Area ABC} \\ &=& \mbox{Area ABC}
\end{eqnarray}$$