Models, images, representations, diagrams. The mathematics education literature is replete with terms suggesting the importance of making mathematical ideas manifest. Common across all these terms is an emphasis on some sort of physicality but I'm not clear about the subtle differences between them. Isn't a diagram an image? Is 'representations' a more encompassing term than 'models'? Does it help to have a range of terms at all? For example, 'models and images' are often 'bundled' together. Presumably this arises from the everyday distinction that models are three-dimensional and images two-dimensional. Models, largely, can thus be 'acted upon'. Images, in this everyday sense, have a more static quality to them - while my eye may roam around the image of the Mona Lisa, I'm not encouraged to pick it up and physically act upon it.

But in the mathematics classroom, number lines, arrays and similar images are to be 'acted upon', so in an attempt to simplify things, I want to lump everything together under the one heading of models, in the sense of a model being something that 'stands-in-for' something else, irrespective of whether it is two- or three-dimensional. Professionals who make models include all sorts of designers - theatrical set designers, architects, furniture makers - where models act as 'proto-types' for the real thing. In the mathematics classroom models can be proto-concepts.

I choose to use model to emphasis the interactive nature of working over the subtly more passive nature of images. And I can engage learners in the actions of modelling (as in creating a model, not walking down the catwalk!) whereas the activity of 'imaging' is more difficult to envisage (although I do value the importance of 'imagining').

Models and tools

With this definition the images and diagrams that learners create and work with become models: quickly sketching an empty number line and using movement along the line to represent addition or subtraction is an act of modelling. The work from the Dutch Realist Mathematics Education at the Freudenthal Institute provides a framework for thinking about how we can help, and monitor, learners working with models. The researchers there distinguish between:
Models of
Models for
Tools for [1]

Classroom artifacts such as number lines, 100 squares or base 10 blocks, start life in the classroom as models of, in the sense that the teacher works with these in ways that imbue the models with meaning before learners may have come to 'read' the models in the same way. To take a simple example, young children have informal strategies for solving addition problems. Adding four and three they may hold out four fingers and then another three and count the total. The teacher could model this by drawing a number line, counting along to four on the line and then counting on three more 'steps' to land on seven. This model of the addition is not a direct mirroring of what the children did: they were counting objects (fingers), the teacher is counting jumps and it takes time for the children to appreciate the links between their activity and that of the teacher.

Through this type of joint activity learners solve problems in their own way and the teacher provides a mathematical model of their solutions, then, over time, the learners begin to appropriate the teacher's model and to use it for themselves; there is a shift from the teacher providing a model of the activity to learners taking this on as model to use themselves.

The Dutch research shows that eventually, if the model is a good one, then learners come to be able to work with the model, but without needing to make actual marks on paper: the model is imagined and has become a tool for thinking with.

This move from model for to tool for is, I think, the key thing to consider when choosing models to introduce into the classroom. For example when I began teaching it was the norm that base-ten blocks were used to teach multi-digit addition and subtraction. Although still around in classrooms they are less prominent than they used to be. That may be because of fashion, but I think it is also to do with this move from model for to tool for: base ten blocks are great to actually manipulate but recent research suggests that they may not be the sort of image that we work with mentally. For example the work of Stanislas Dehaene suggests that the mind deals with numbers more akin to ordinal models - the number line - than cardinal models - piles of bricks [2].

Tools for reasoning with

A mark of a good model for/tool for thinking with is that it can help learners gain insight into mathematical structure, not simply get correct answers. Here is where base ten blocks can provide a helpful model. Rather than the teacher modelling how to exchange, say, ten ones cubes for a single ten stick by counting out and swapping, the cubes could be used to model the powers of ten structure of the place value system. Handling and talking about the cubes in ways that invite learners to imagine that a single cube is scaled up by a factor of ten to make a ten stick which similarly is scaled up by a factor of ten to make a hundred 'flat' and so forth encourages learners to 'read' the cubes in this multiplicative fashion rather then additively (as the count out and exchange modelling encourages). It is then easier to use the cubes to model the decimal system by extending the idea of scaling up to scaling down to become ten times smaller.

As this example shows, we mustn't assume that the mathematics is 'in' a model simply waiting to be recognised or discovered. The mathematics that emerges depends upon what features of the model are stressed or ignored, to use John Mason's terms [3]. Stressing the 'scale' properties of base ten blocks means playing down the additive properties. This is where the role of the 'significant' other that Vygotsky raised becomes important. A sensitive other (and that may be a peer as much as the teacher) will gradually lead the learner to this noticing, in ways that hopefully encourage an 'aha' moment of insight.

Part of provoking 'stressing' comes through careful choice of examples. Suppose a learner is able to work out mentally that 200 − 165 = 35. Given 212 − 177 they may have to work that out differently, perhaps using paper and pencil, as it does not look immediately as amenable to a mental calculation as 200 − 165. Getting, again, the answer 35, the learners who throughout their mathematics lessons have been encouraged to stress looking for patterns (even though equal results may simply be coincidental) are encouraged to pause and set up a quick model to check out if there is a relationship between the two answers. The empty number line provides a model that supports thinking about what is going on. Setting up the initial condition of 200 − 165 as finding the difference between the two numbers (as opposed to 'taking away' the 165 from 200) gives an initial model to play with:

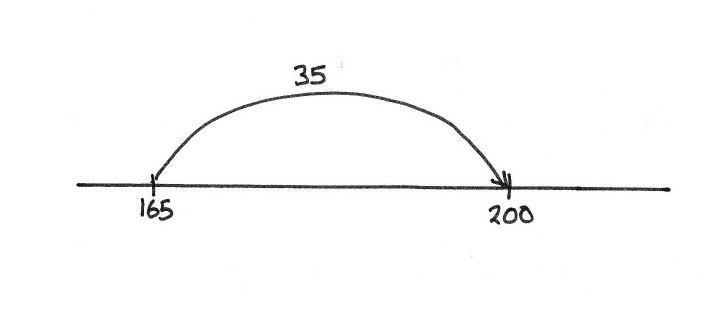
Putting the difference between 212 and 177, perhaps below the line to keep things clear, has the potential for the learner to notice that as the 200 and 165 were both increased by 12, then the difference between the two new numbers must be the same.

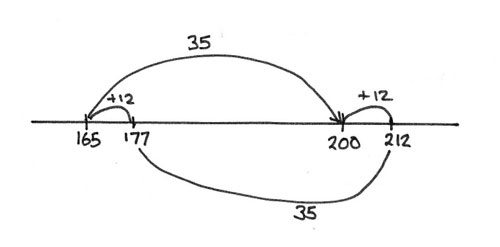
This 'noticing' is an active attending to the model - the learners' attention has to be primed to look for connections - the model does not in and of itself make the connection obvious (in contrast to the way that, as I write, my attention has just been drawn by the sound on the roof that it has started raining). Mind and model thus interact in bringing the mathematics into being - constant difference, in this example, is not 'in' the model waiting to be 'discovered' any more than it is 'in the mind' waiting to be revealed. The skill in teaching here is the subtle focusing of the learners attention so that they experience that moment of insight: 'Aha, of course the answer must be the same, as each number has been made equally larger'. On the other hand, too much 'scaffolding' and there is a danger of provoking a 'duh' moment instead: 'Duh, why didn't I notice that?'

Rich models

There's encouragement in the literature to expose learners to a range of models. While there is no doubt that any one model will have limitations, my work with teachers suggests that this encouragement to introduce a variety of models is sometimes interpreted differently; that if learners don't 'get it' with a particular model, try a different one. As indicated above the Dutch research shows that 'getting it' takes time and that we shouldn't abandon models too soon. The question to ask when choosing models is less one of how many models to introduce and more one of how 'rich' a model is in its potential to extend into different aspects of mathematics. The array is one such particularly rich model.

The power of arrays

Arrays are beginning to be used quite a lot in introducing multiplication and in the 'grid' method as a bridge to introducing the algorithm for multi-digit multiplication. But the potential of arrays does not end there.

The array can also be used to help make clear the link between multiplication and division. Suppose you want to figure out 176 ÷ 8. We can set this up as an array with the value of one side missing.

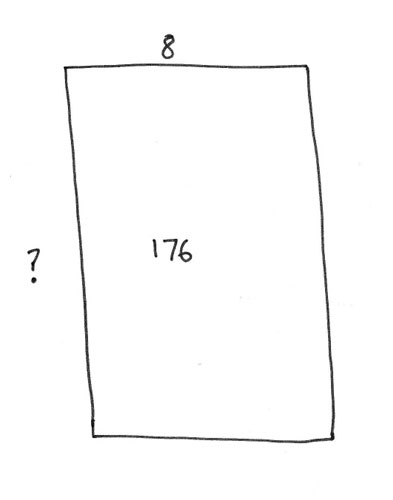
Using known multiplication facts the value of the missing side can be built up.

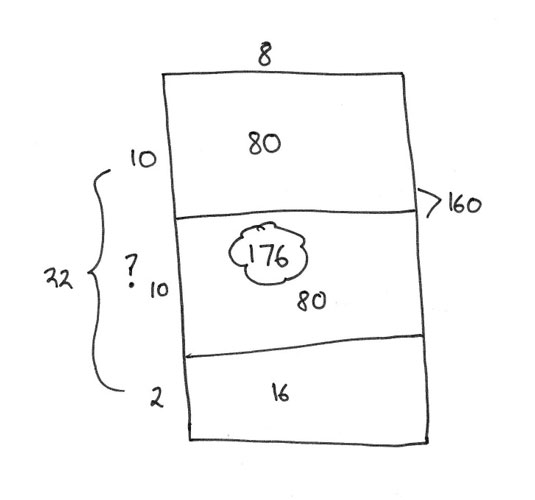
And what about fractions? Consider for example the calculation 2/3 x 2/5. Learners brought up on 'multiplication as repeated addition' can come unstuck when faced with such a calculation - how can you add 2/3 two-fifth number of times. A quick sketch of an array can move things forward. Start with an array that is divided into thirds one way and fifths the other.

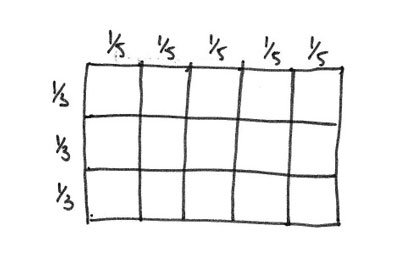
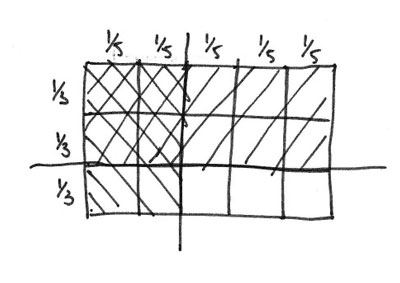
Learners who have come to think of multiplication in terms of arrays will be comfortable in thinking of the required piece as being the part of the array marked out by the intersection of the 2/3 and 2/5.

Finally, here's an insight from working with this model that I only recently came across. Take the calculation 7/8 x 4/7. The array model looks like:

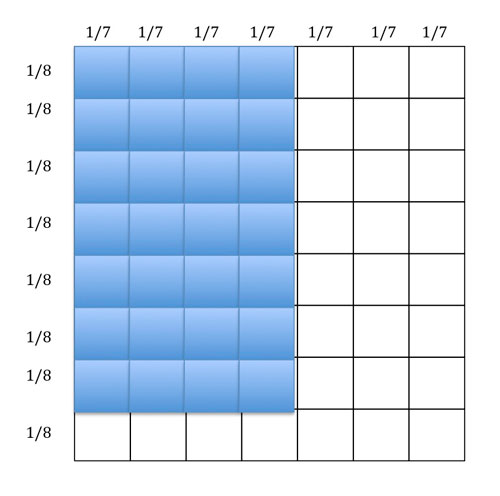
From this we can see that the overall array has been divided into 8 x 7 smaller parts, hence the denominator is 56. And the shaded part is 7 x 4 = 28. So the answer is 28/56 or 1/2. So far, this may seem like a sledgehammer to a nut, but here's the insight. We can take, in our imagination, the shaded part of the array and, without damage to the calculation, rotate it through 90 degrees.

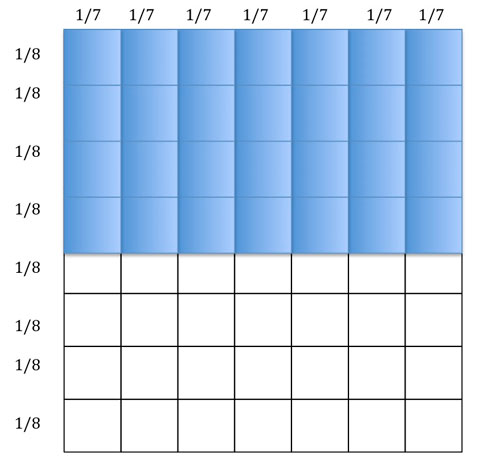
Now we can see the answer 1/2; quite clearly. And more. What this manipulation of the model establishes, is that when multiplying two fractions it's ok to swap over the numerators - the answer will be the same. So 7/8 x 4/7 = 4/8 x 7/7 = 1/2 x 1 = 1/2. Neat eh?

References

1. Gravemeijer, K., How emergent models may foster the constitution of formal mathematics. Mathematical Thinking and Learning, 1999. 1(2): p. 155-177.
2. Dehaene, S., The number sense: How the mind creates mathematics. 1999, Oxford: Oxford University Press.
3. Mason, J., Burton, L. & Stacey, K. Thinking Mathematically. 2010. 2nd edition. Harlow: Pearson Education Ltd.

Here is a PDF version of this article.