Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Kite in a Square
Age 14 to 18
Challenge Level 





Kite in a Square printable sheet
ABCD is a square. M is the midpoint of the side AB.
By constructing the lines AC, MC, BD and MD, the blue shaded quadrilateral is formed:
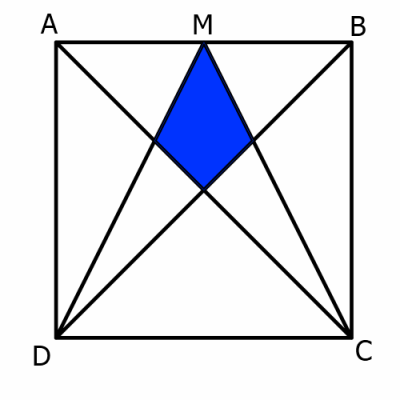
What fraction of the total area is shaded?
Once you have had a think about this, you might like to take a look at these three different methods for finding the shaded area. In each case, all the statements have been muddled up. Can you rearrange them back into their original order?
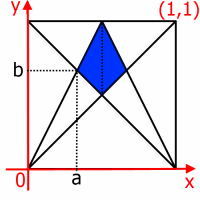
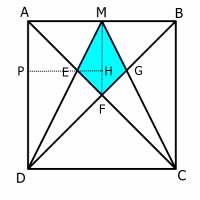
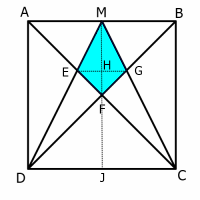
Thanks to Jerome Foley for drawing our attention to this problem.
We are very grateful to the Heilbronn Institute for Mathematical Research for their generous support for the development of this resource.