If you double the sides of a square, the area becomes four times the size. It is quadrupled.

We can try the same thing with a rectangle and a rhombus.

How do the four smaller ones fit into the larger one?

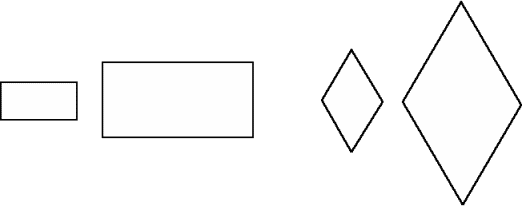
We can then try with equilateral triangles:

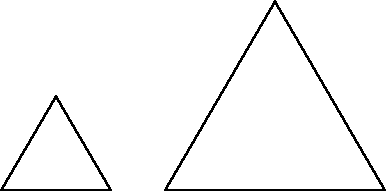
And "L" shapes:

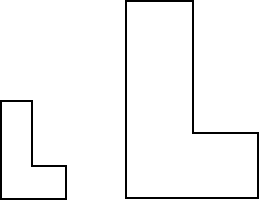
What has to be done to make these fit?

We could try with other shapes like hexagons.
These have to be cut and rearranged.

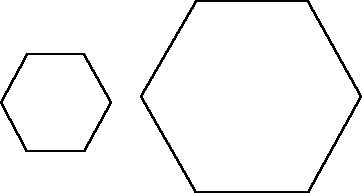
What is the least number of cuts needed to fit four hexagons into one larger hexagon with sides double the length?