Bracelets

Well, in this country, and perhaps in yours, lots of young folk are wearing bracelets - both girls and boys. I was looking at some that my students wear and found that some were magnetic!

Many seem to have beads that are spherical and they go around the wrist quite comfortably. There are lots of different sizes and some have large beads and some quite small beads.

I suppose that most wrists are kind of oval - squashed circles - in shape and with the string or wire through the beads they fit very well.

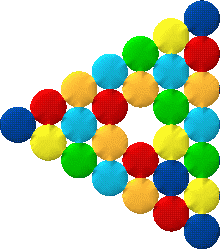
It was playing with the magnetic beads off the person's wrist that gave me some ideas. There were $18$ beads altogether and they were all the same colour but I've chosen to show them in a variety of colours!

I found I could put them into different shapes:-

mind you, you'd have to have a triangular wrist for them to stay like that!

Now suppose we play around with this idea and make a rule that there has to be some shaped hole in the middle for a wrist. But we'll allow that to be all kinds of shapes :- vaguely triangular, rectangular, hexagonal etc.

You could try this out with marbles, circular counters, tiddly-winks, coins or with a drawing program on your computer.

I think we'll make a rule that the circles/spheres have to be the same size and you don't have to imagine that they're magnetic!

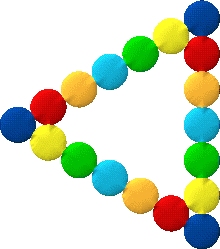
So here are some that I found with $18$ beads:-

I liked that one as it is the longest rectangle you could make - remembering to keep a wrist-hole. I then went on to:-

and then, almost a square :-

I like the next one - although it was a little hard to do on the computer!

Have a go at making these with your circles!

Well, now it's time to explore, to see what other bracelets you can make. Remember that there's to be a "wrist-hole". The shapes should be kind of "regular" but not strictly so, because then we could not use rectangles.

Other things to investigate:-

1. If you make a particular shape with $18$ and then the next size up comes when you use $24$, is there going to be the next size up at $30$?

   So whatever shape you make, how many will you need to make the next size up? How does each shape grow? Look at the first shape I made using $24$:-

   
   
   

   What will the next size up of this look like?

2. What are good numbers of beads to use? Why?
3. What's the smallest number of beads that will allow you to make two identical bracelets? Why? How many will you need to make three of those?
4. If you make a bracelet with just one thickness of beads them how many will you need to make one that has a double thickness? Here's one I did by making the wrist-hole smaller and getting it to be twice as thick:
   
   
   
5. Would cube beads lend themselves to exploring slightly differently? What about tetrahedral bead?
6. What about ...?