Copyright © University of Cambridge. All rights reserved.
'Stadium Sightline' printed from https://nrich.maths.org/
Show menu
One of the challenges in designing an Olympic stadium is to make sure that spectators can see the event without their views being blocked by the spectators in front.
Your task is to design the tiered seating for the stadium. The back of each seat is 80cm behind the back of the seat in front, but raised up so that each row can see over the row in front.
Make some sketches showing what the cross-section (side view) of the seats might look like. Will the seats lie on a straight line, or a curve? How steep?
What factors do you think you will need to take into account when working out how high each seat needs to be?
The Olympic organisers have stipulated that all spectators must be able to see clearly a point 10m in front of the front row of seating:
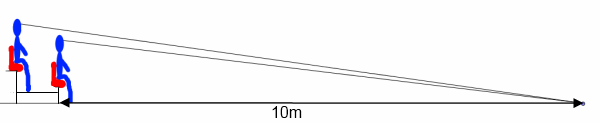
The spectator in the second row needs to have line of sight to the same point as the spectator in the first row, as seen in the diagram above. Notice that the spectator in the second row needs some extra clearance in order to see comfortably over the first spectator's head.
Here is a zoomed-in diagram:
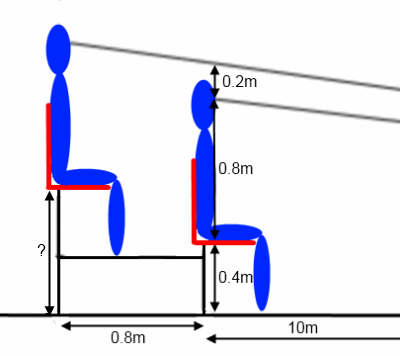
The first spectator's eye-level is 1.2m above the ground.
There is an extra 0.2m of clearance from his eye-level to the second spectator's line-of-sight. The second spectator is a further 0.8m away from the point on the pitch.
How high above ground level does spectator 2's seat need to be?
Now draw a similar diagram with the dimensions and unknowns for spectators 2 and 3.
How high above ground level does spectator 3's seat need to be?
Finally, imagine there were 40 rows of seating in the stadium.
Can you work out the heights above ground level of each of the 40 rows, and hence plot a side view of the seating?
It is very helpful to use a spreadsheet to perform the repeated calculations and plot the results.