Copyright © University of Cambridge. All rights reserved.
'Irrational Arithmagons' printed from https://nrich.maths.org/
Show menu
In a multiplication arithmagon, the number on each edge of the arithmagon is the product of the numbers at the adjacent vertices.
You may wish to look at Multiplication Arithmagons and develop a general strategy for working out the numbers at the vertices, given the edge numbers, before tackling the question below.
Can you work out the numbers that belong in the circles to make this multiplication arithmagon correct?
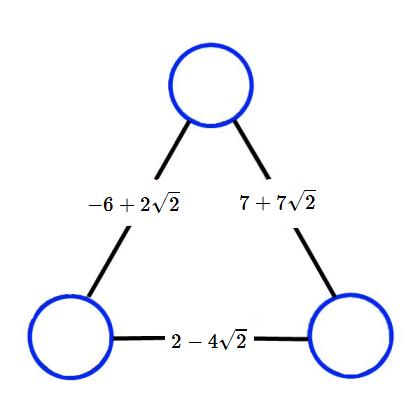
If you're not sure where to start, click for a series of hints:
Each circle will be of the form $a+b\sqrt2$ for some values of $a$ and $b$.
In general, a multiplication arithmagon can be solved by multiplying, dividing, and square-rooting.
Dividing an expression by $a+b\sqrt2$ is the same as saying, "What must I multiply $a+b\sqrt2$ by to get that expression?"
To find the square root of an expression such as $12-8\sqrt2$, consider the equation $(x+y\sqrt2)^2=12-8\sqrt2$, expand the brackets, and deduce $x$ and $y$.