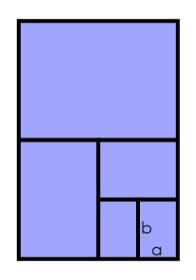
Charlie took a sheet of paper and cut it in half.

Then he cut one of those pieces in half, and repeated until he had five pieces altogether.
 
He labelled the sides of the smallest rectangle, $a$ for the shorter side and $b$ for the longer side.







Here is a shape that Charlie made by combining the largest and smallest rectangles: 
 
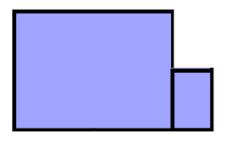
Check you agree that the perimeter is $10a + 4b$.

Alison combined the largest and smallest rectangles in a different way. Her shape had perimeter $8a + 6b$. Can you find how she might have done it?

Charlie and Alison made sure their rectangles always met along an edge, with corners touching.
Can you combine the largest and smallest rectangles in this way to create other perimeters?
 
Create some other shapes by combining two or more rectangles, making sure they meet edge to edge and corner to corner. What can you say about the areas and perimeters of the shapes you can make?

If you have a friend to work with, you could each create a shape and work out the area and perimeter. Can you recreate each other's arrangement if you only know the area and perimeter?
  
Here are some questions to consider:

What's the largest perimeter you can make using ALL the pieces? 
 
Can you make two different shapes which have the same area and perimeter as each other?
 
Can you make two different shapes which have the same perimeter but different areas? 
 
How do you combine any set of rectangles to create the largest possible perimeter?

Charlie thinks he has found a shape with the perimeter $7a + 4b$. Can you find his shape? 

What can you say about the perimeters it is possible to make, if $a$ and $b$ are the dimensions of one of the other rectangles?

This problem is based on an idea shared by Sue Southward.