Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Follow the Numbers



This is your chance to follow some numbers and see where they go!
A simple rule is all you need.
My first suggestion is to add the digits together then multiply (times) by $2$.
The first number that I chose happened to be $56$.
So, let's start:
We add the $5$ and $6$, $5+6=11$
We multiply the $11$ by $2$, $2 \times 11 = 22$, and that's the first part of the journey.
So, where now?
We carry on with this rule:
We add the $2$ and $2$, $2+2=4$
We multiply the $4$ by $2$, $4\times 2 = 8$, and that's the second part the journey.
Now, $8 + 0 = 8$ and $8\times 2 = 16$ and that was the third part.
And, $1 + 6= 7$, and $7\times 2 = 14$
Do the same to $14$ and we get $10$
$10$ leads to $2$, $2$ leads to $4$, $4$ leads to $8$ and we are back to where we got to in the second part of the journey.
If we went on and on and wrote down where we got to after each part we would see something like:
$56, 22, 8, 16, 14, 10, 2, 4, 8, 16, 14, 10, 2, 4, 8, ...$
After exploring that journey it's time to start somewhere new, for example $11$ which goes along like this;:
$11, 4, 8, 16, 14, 10, 2, 4, 8, ...$
Oh! So we are on the same bit as before, a circular bit that goes $2, 4, 8, 16, 14, 10$ and then back to the $2$ again.
Now a new starting place, $96$.
This goes like this:
$96, 30, 6, 12, 6, 12, 6, ...$
Oh! So we now have a smaller circular bit of the journey that goes $6, 12$ then back to the $6$.
I explored further trying to start with each number from $1$ to $99$.
Then I tried similar, but different rules.
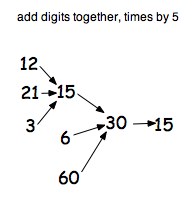
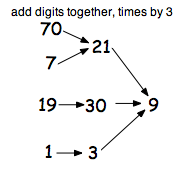
I found I needed a big piece of plain paper and used arrows to show the journeys. Here are just some bits of them to tempt you to go further:
 and
and