Links to the University of Cambridge website
 Links to the NRICH website Home page
Links to the NRICH website Home page

 Links to the NRICH website Home page
Links to the NRICH website Home page

Nurturing young mathematicians: teacher webinars
30 April (Primary), 1 May (Secondary)
30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Turning to Calculus
Age 16 to 18
Challenge Level 





The following curve turns once. It changes sign twice and the sign of its gradient changes once, giving rise to four distinct regions, as shown in the image below:
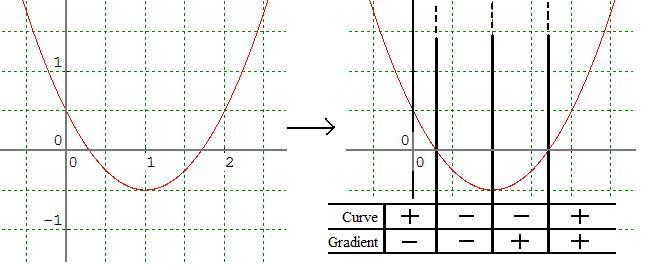
What are the different possibilities of sign combination for a
curve which turns exactly once? How can you be sure you have found
them all? Give a clear explanation.
Which are the different possibilities of sign combination for a curve which turns exactly twice? How can you be sure you have found them all? Give a clear explanation.
Explore other numbers of turns and the curves which give rise to various numbers of regions.
It is not intended that you use algebra; simply experiment with sketches and focus on clear mathematical reasoning.
Further
extensions:
Once you have a good feel for the
setup, you might wish to think about these more tricky or general
questions:
1. Are there any curves which
always have the same sign for the function and gradient?
2. Are there any curves which
always have the opposite sign for the function and gradient?
3. Are there any impossible
combinations of sign?
4. How do zeros of the function
and zeros of the gradient enter into the analysis?
5. Find algebraic expressions
for any functions you use in this problem.