Consider the Venn diagram for 3 sets $A$, $B$ and $C$ with each of the $7$ regions labelled as follows
 
 
 
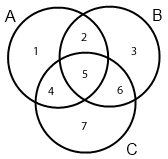
The set-theoretic representation of these regions is
 
1. $C^c\cap B^c$
 
2. $A\cap B \cap C^c$
 
3. $A^c \cap C^c$
 
4. $A\cap C \cap B^c$
 
5. $A\cap B\cap C$
 
6. $B\cap C \cap A^c$
 
7. $A^c \cap B^c$
 
 
A four-region diagram can be constructed by overlapping four rectangles (blue, pink, yellow, red) as follows:
 
 
Note that there are $15$ distinct regions of the diagram, corresponding to $2^4-1$. Make sure your diagram has exactly 15 regions!