Olivia from Roedean in the UK sent this work on modulo 5 and 7:

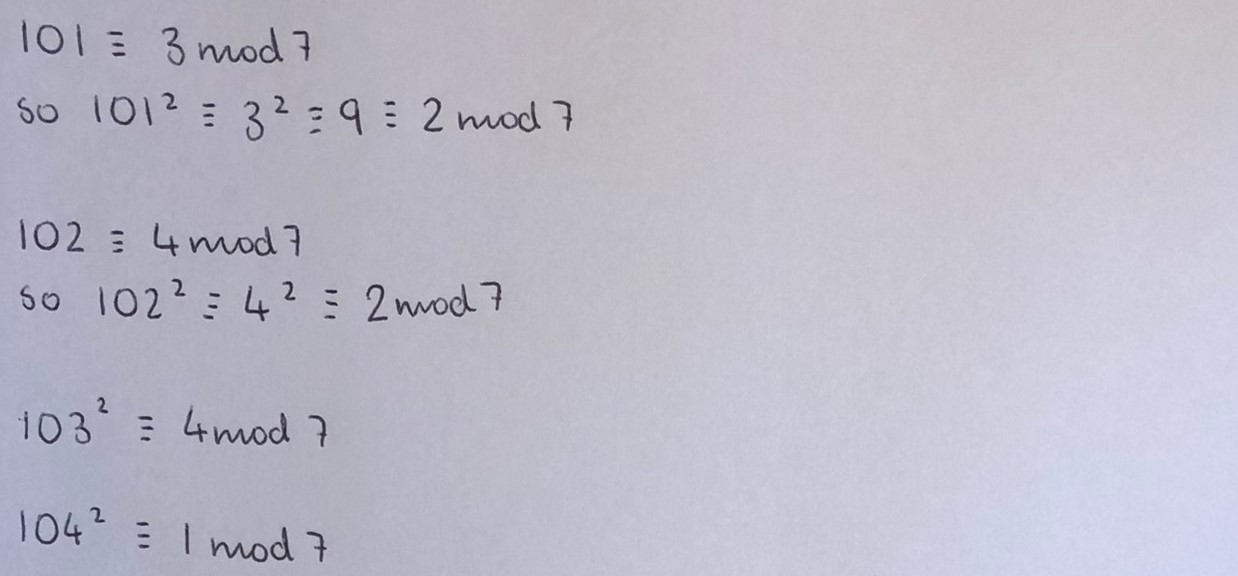
Olivia mentioned the problem More Adventures with Modular Arithmetic.

Mahdi from Mahatma Gandhi International School in India and Olivia tried more prime numbers. Mahdi made this table. Click here to see a larger version.

Mahdi noticed the same pattern that Olivia used to find 100², 101², ... mod 5 and mod 7, as well as another pattern:

The very first thing I notice is how similar patterns emerge from $n$ mod $p$ and $n^2$ mod $p.$
The values modulo prime numbers, also repeat in the same interval. So, for example, the column with 5 has remainders that repeat after every 5 integers. Same goes with 7, 11, 13 and 17. Also, excluding the zero, I noticed that the “block” (That is highlighted in bold for each column) is symmetrical from the top and bottom.

Martin from Prague British International School Prague Libuš in the Czech Republic and Olivia noticed this symmetry and explained how it can be used to predict the rest of the squares. Martin wrote:

The formula $p=2x+1$ works in finding the amount of values [you need to know before you can predict all the squares].

By using the example of mod7, $p$=7. So 7=2$x$+1, which means $x$ will be 3. $x$ refers to the number of values we need to know before we can predict the rest.
If $x$=3 that means the there will be 3 numbers that we need to know, before they are repeated in reverse. The numbers are 1,4,2 (then they continue in reverse),2,4,1… (and these numbers repeat forever)

1² = 1 ≡ 1 mod 7
2² = 4 ≡ 4 mod 7
3² = 9 ≡ 2 mod 7

4² = 16 ≡ 2 mod 7
5² = 25 ≡ 4 mod 7
6² = 36 ≡ 1 mod 7

Olivia used algebra to prove that this will always happen:

Mahdi proved this in a slightly different way and then used ideas from the proof to find 101² mod 5. Notice that Mahdi uses $a$ to refer to each of the numbers on the list. It is more common to use a different letter or symbol for each number, such as $a_0, a_1, a_3, ... a_{p-1}.$

Mahdi and Olivia also looked at mod $n$ for $n$ even. This is Mahdi's table (see a larger version here): 

Olivia proved that there is a similar pattern to before:

Mahdi also noticed that, for modulo $n$ where $n$ is not prime, some numbers have squares equal to zero. This is Mahdi's work: