Clock Squares
This problem follows on from Clock Arithmetic and More Adventures with Modular Arithmetic.
Start by considering square numbers in modulo $5$.
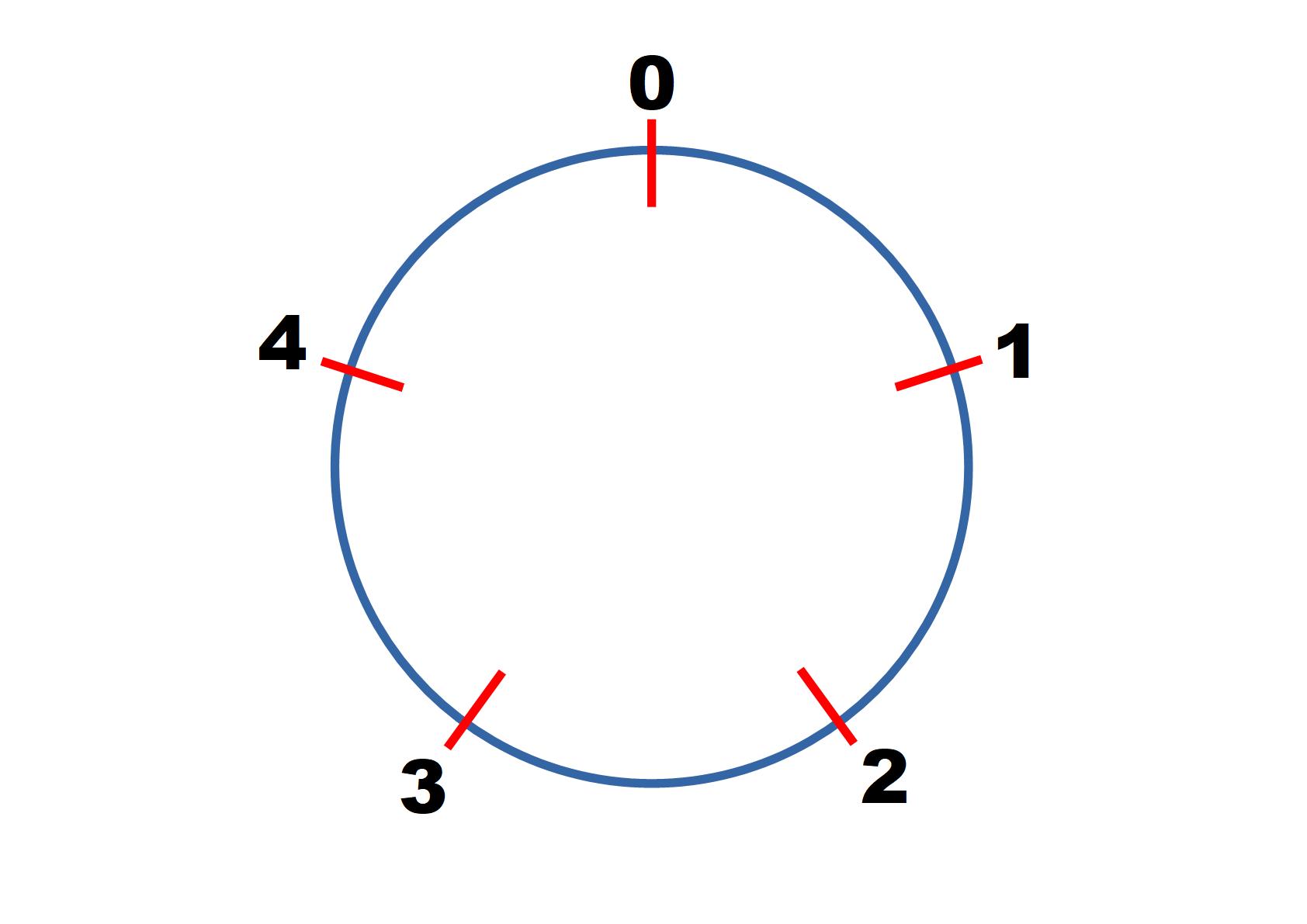
$1^2 = 1 \equiv 1 \text{ mod } 5$
$2^2 = 4 \equiv 4 \text{ mod } 5$
$3^2 = 9 \equiv 4 \text{ mod } 5$
$4^2 = ...$
$5^2 = ...$
Continue finding the value of other square numbers in modulo 5 until you notice a pattern and can predict correctly what will come next.
Can you predict the values of $100^2, 101^2, 102^2...\text{ in mod } 5$?
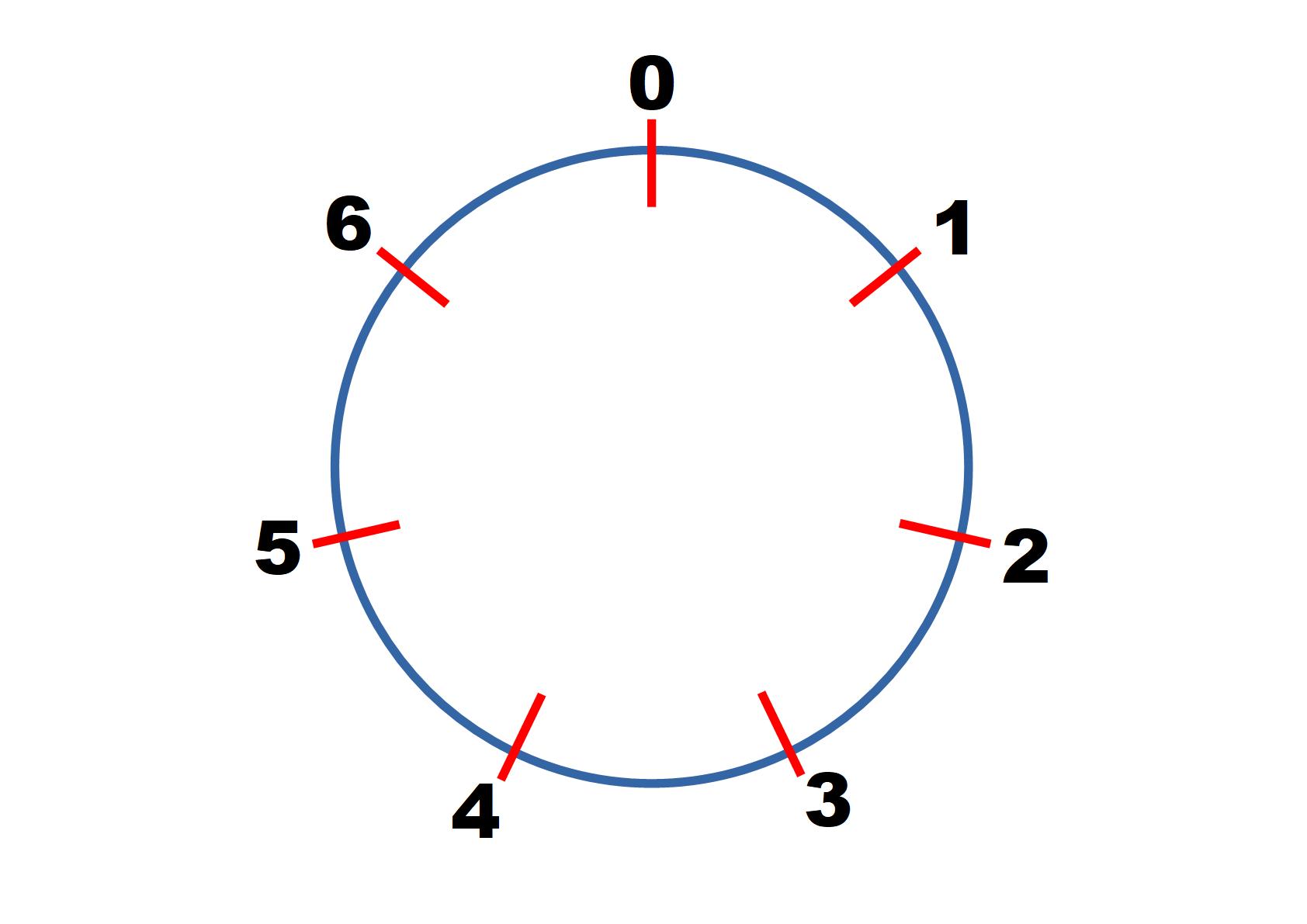
In modulo $7$ we have:
$1^2 = 1 \equiv 1 \text{ mod } 7$
$2^2 = 4 \equiv 4 \text{ mod } 7$
$3^2 = 9 \equiv 2 \text{ mod } 7$
$4^2 = 16 \equiv 2 \text{ mod } 7$
Continue finding the value of other square numbers in modulo 7 until you can predict correctly what will come next.
Can you predict the values of $100^2, 101^2, 102^2...\text{ in mod } 7?$
Investigate the value of other square numbers in modulo $11, 13, 17$...
You may find this power modulo calculator useful!
When working in mod $p$, where $p$ is prime, how many values do you need to find before you can predict all the rest? Explain your findings.
Can you predict any values from the very start?
So far you have looked at square numbers modulo $p$, where $p$ is a prime.
Investigate square numbers modulo $n$, where $n$ is odd but not prime, or where $n$ is even.
If you have enjoyed working on this problem, then you may enjoy Euler's Totient Function.
We are very grateful to the Heilbronn Institute for Mathematical Research for their generous support for the development of this resource.
If you have already met More Adventures with Modular Arithmetic then you will have learnt that if $A \equiv a \text{ mod } n$ and $B \equiv b \text{ mod } n$ then $AB \equiv ab \text{ mod } n$.
This means that since $23 \equiv 2 \text{ mod } 7$ we have $23^2 \equiv 2^2 \text{ mod }7$ and so $23^2 \equiv 4 \text{ mod }7$.
Olivia from Roedean in the UK sent this work on modulo 5 and 7:
Olivia mentioned the problem More Adventures with Modular Arithmetic.
Mahdi from Mahatma Gandhi International School in India and Olivia tried more prime numbers. Mahdi made this table. Click here to see a larger version.
Mahdi noticed the same pattern that Olivia used to find 1002, 1012, ... mod 5 and mod 7, as well as another pattern:
The very first thing I notice is how similar patterns emerge from $n$ mod $p$ and $n^2$ mod $p.$
The values modulo prime numbers, also repeat in the same interval. So, for example, the column with 5 has remainders that repeat after every 5 integers. Same goes with 7, 11, 13 and 17. Also, excluding the zero, I noticed that the “block” (That is highlighted in bold for each column) is symmetrical from the top and bottom.
Martin from Prague British International School Prague Libuš in the Czech Republic and Olivia noticed this symmetry and explained how it can be used to predict the rest of the squares. Martin wrote:
The formula $p=2x+1$ works in finding the amount of values [you need to know before you can predict all the squares].
By using the example of mod7, $p$=7. So 7=2$x$+1, which means $x$ will be 3. $x$ refers to the number of values we need to know before we can predict the rest.
If $x$=3 that means the there will be 3 numbers that we need to know, before they are repeated in reverse. The numbers are 1,4,2 (then they continue in reverse),2,4,1… (and these numbers repeat forever)
12 = 1 ≡ 1 mod 7
22 = 4 ≡ 4 mod 7
32 = 9 ≡ 2 mod 7
42 = 16 ≡ 2 mod 7
52 = 25 ≡ 4 mod 7
62 = 36 ≡ 1 mod 7
Olivia used algebra to prove that this will always happen:
Mahdi proved this in a slightly different way and then used ideas from the proof to find 1012 mod 5. Notice that Mahdi uses $a$ to refer to each of the numbers on the list. It is more common to use a different letter or symbol for each number, such as $a_0, a_1, a_3, ... a_{p-1}.$
Mahdi and Olivia also looked at mod $n$ for $n$ even. This is Mahdi's table (see a larger version here):
Olivia proved that there is a similar pattern to before:
Mahdi also noticed that, for modulo $n$ where $n$ is not prime, some numbers have squares equal to zero. This is Mahdi's work:
Why do this problem?
This problem follows on from Clock Arithmetic. It gives students the opportunity to consider what happens when we square numbers in modular arithmetic. It gives students the opportunity to work systematically and to spot patterns.
Possible approach
This problem featured in an NRICH Secondary webinar in April 2021.
To start with students could be asked what the values of $1^2$, $2^2$, $3^2$ and $4^2$ are modulo $5$. Can they state what $5^2 \text{ mod } 5$ is without evaluating $5^2$? Can they predict what $6^2, 7^2$ etc are modulo $5$?
Students could work in pairs to find square numbers in different modulos, and it might be useful to start by only considering prime number modulos. Encourage students to collect their results in a table and to start to look for patterns. Challenge them to predict what the pattern will look like for a new modulo and test their predictions.
Students can then go on to investigate square numbers in modulos that are odd but not prime, or which are even.
Key questions
Which values of $x$ satisfy $x^2 \equiv 0 \text{ mod }n$?
When working in modulo $p$, where $p$ is prime, how many different values of $x^2 \text{ mod } p$ are there?
Possible support
Students could start by working on Clock Arithmetic.
Students should be encouraged to work systematically and to lay out their results logically, possibly in a table.
Possible extension
If they have not already done so, students might like to move onto More Adventures with Modular Arithmetic. They might also like to investigate Euler's Totient Function.
Further reading on modular arithmetic can be found here