Answer: 92 squares


Building the tenth pattern in rectangles
  ...   

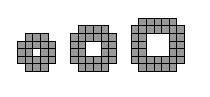                                                                                      Total 23$\times$4 = 92 squares


Building the tenth pattern from a larger square
 

Each large square has the centre and corners removed

14$^2-$ 10$^2-$ 4 = 196 $-$ 100 $-$ 4 = 92


Using smaller rectangles and algebra

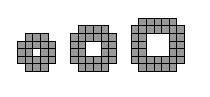
Break the pattern down into four rectangles, each two squares wide, and four L-shaped corner pieces, of three squares each.

Pattern 1 = $4 \times 2 \times 1 + 4 \times 3 = 20$

Pattern 2 = $4 \times 2 \times 2 + 4 \times 3 = 28$

Pattern 3 = $4 \times 2 \times 3 + 4 \times 3 = 36$

Pattern n = $4 \times 2 \times n + 4 \times 3 = 8n +12$

Pattern 10 = $4 \times 2 \times 10 + 4 \times 3 = 92$ squares


Using larger squares and algebra
Imagine a large square with corners removed, and a square removed from the middle:

Pattern 1 = $5^2 - 4 - 1^2 = 20$

Pattern 2 = $6^2 - 4 - 2^2 = 28$

Pattern 3 = $7^2 - 4 - 3^2 = 36$

Pattern n = $(n+4)^2 - 4 - n^2 = 8n +12$

Pattern 10 = $14^2 - 4 - 10^2 = 92$ squares