 Links to the NRICH website Home page
Links to the NRICH website Home page

30 April (Primary), 1 May (Secondary)
Or search by topic
Number and algebra
Geometry and measure
Probability and statistics
Working mathematically
For younger learners
Advanced mathematics
Pythagoras Proofs



Pythagoras' theorem states that:
If a triangle with sides $a, b, c$ has a right-angle, and $c$ is the hypotenuse,
$a^2+b^2=c^2$
Here are three different diagrams which can be used to prove Pythagoras' Theorem.
Can you make sense of them?
Which proof do you find most "convincing"?
Which do you find easiest to understand?
Method 1:
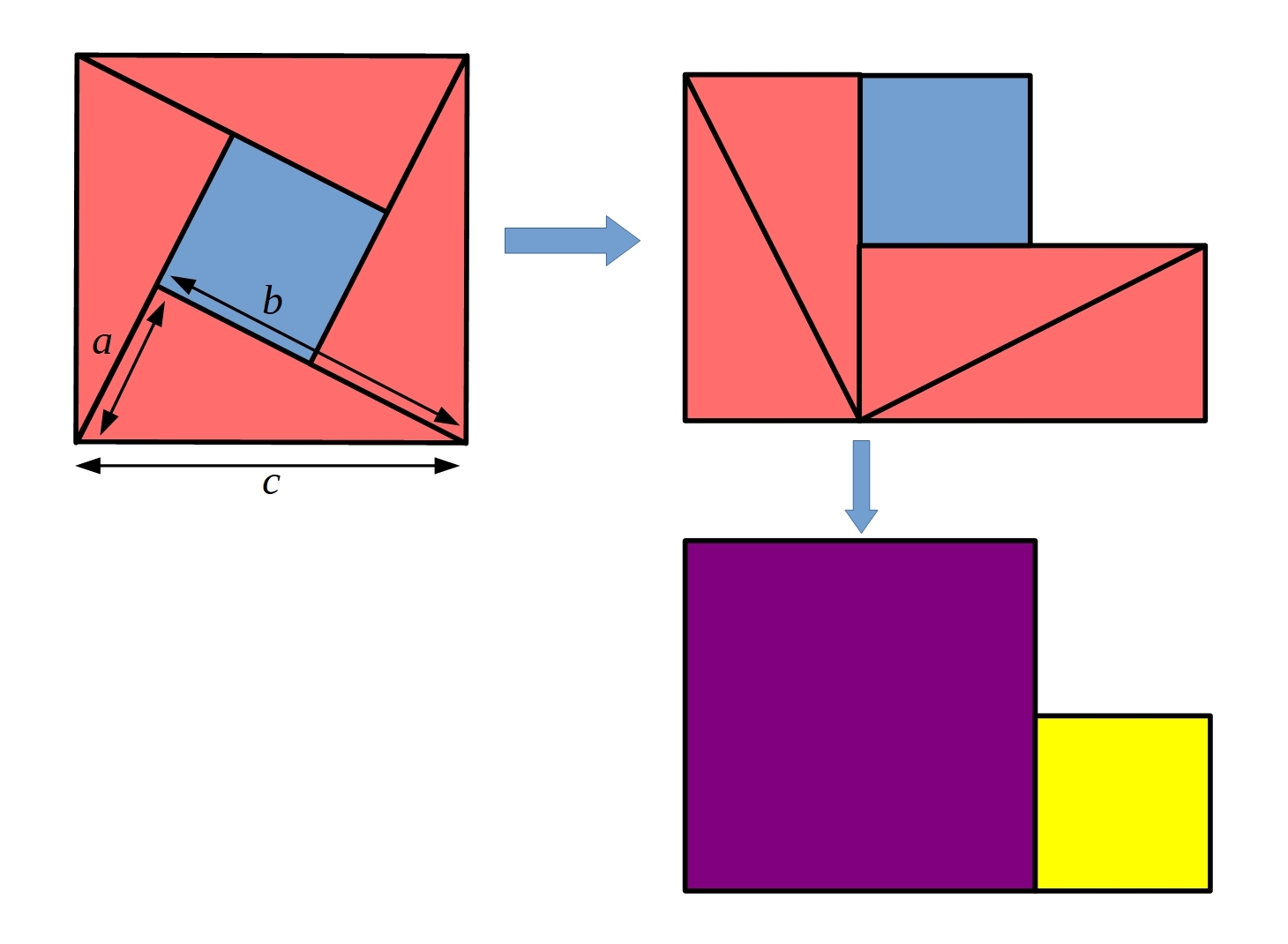
Can you use the picture below and the proof sorter to create a proof of Pythagoras' theorem?
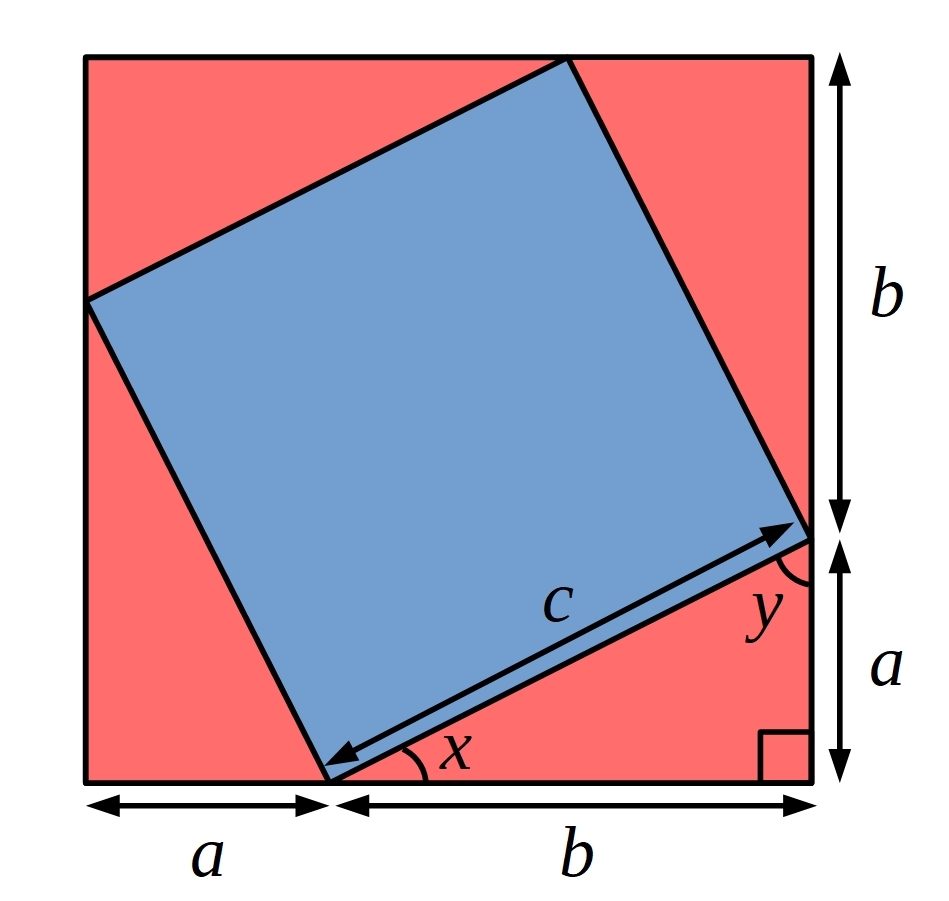
Method 2:
Can you use the picture below to come up with another proof of Pythagoras' theorem?
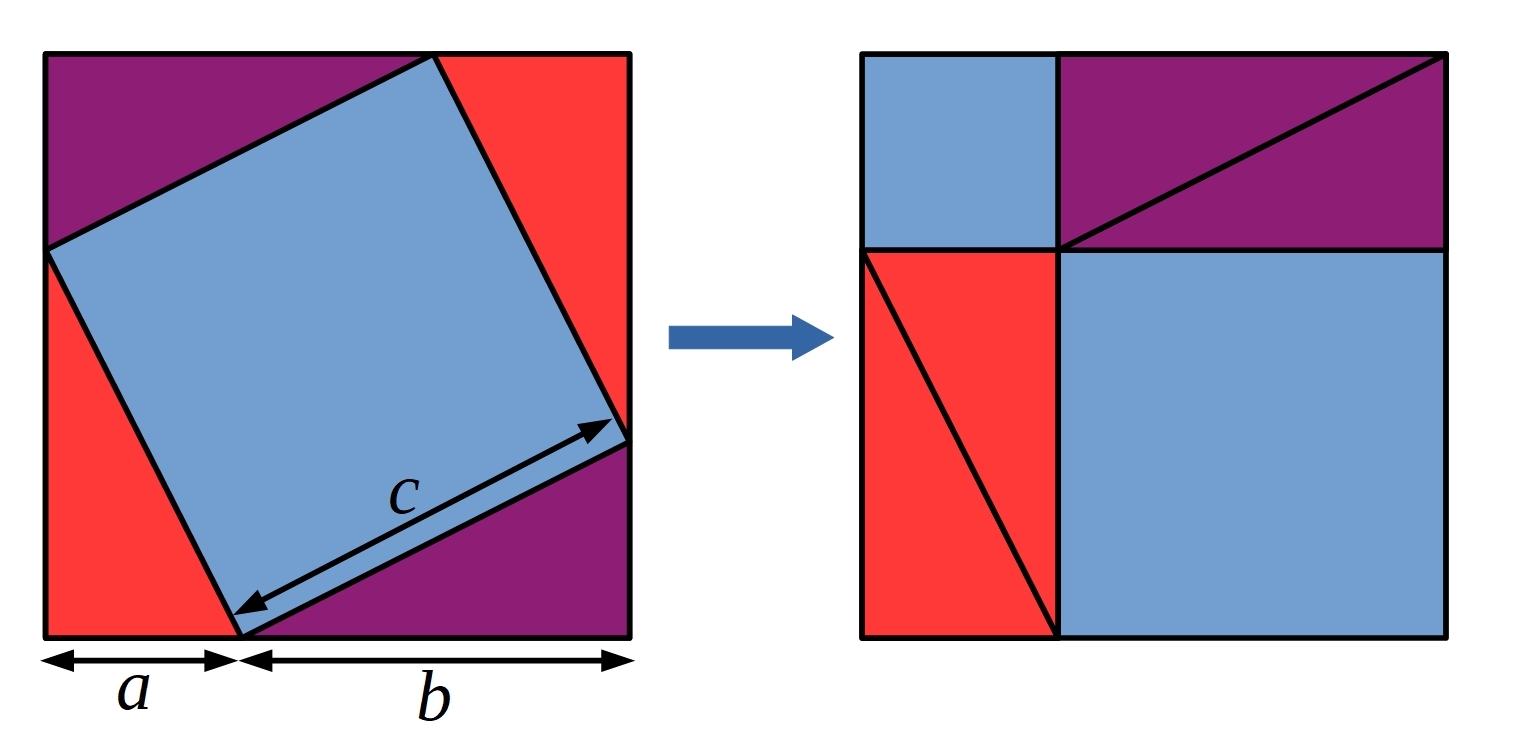
Method 3:
This time the four right-angled triangles have been arranged in a different way. Can you use this picture to create a third proof of Pythagoras' theorem?
Method 4: Another method of proving Pythagoras' Theorem can be found in the problem "A Matter of Scale"
You might also like to explore the problem "The Converse of Pythagoras"
You can find some videos and apps illustrating methods 2 and 3 in this Plus article "Seeing Pythagoras"
If you can find a different proof of Pythagoras' Theorem then please do let us know by submitting it as a solution.
You may also like
Adding All Nine
Make a set of numbers that use all the digits from 1 to 9, once and once only. Add them up. The result is divisible by 9. Add each of the digits in the new number. What is their sum? Now try some other possibilities for yourself!
Doodles
Draw a 'doodle' - a closed intersecting curve drawn without taking pencil from paper. What can you prove about the intersections?