Miraya from Heckmondwike Grammar School in the UK and Ci Hui from Queensland Academy of Science Mathematics and Technology in Australia did some trials, and both concluded that the two reflections must come first. Ci Hui wrote down each trial, and for each trial, Ci Hui noted the images of two points on the line under each transformation and the algebraic effect of the transformation. Here is Ci Hui's work:

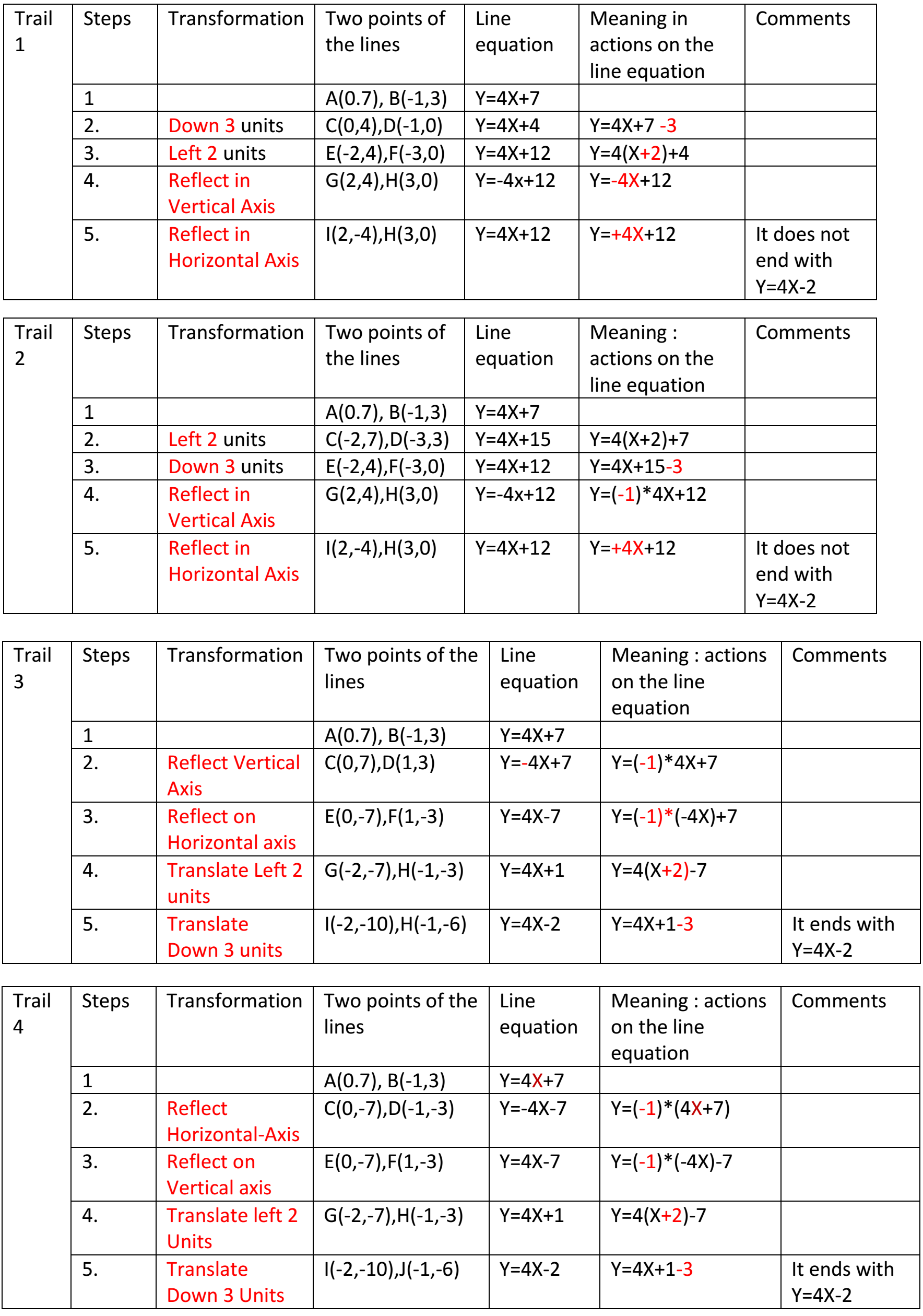
Miraya found four sequences using the same idea:

The first two steps should be reflecting in the x and y axis. There are 4 different orders in order to get the same line:

• Reflect x , reflect y, down 3, left 2 
• Reflect x, reflect y, left 2, down 3
• Reflect y, reflect x, down 3, left 2
• Reflect y, reflect x, left 2, down 3

However, Lynn from Japan found a sequence of transformations that took the line $y=4x+7$ to the line $y=4x+2$ without using both reflections first. Here is Lynn's work:

First, reflect on the [vertical] axis, then translate left by 2 units, then reflect on the [horizontal] axis, and finally translate down by 3 units. 
We start off with $y = 4x + 7.$ I just converted it to $f(x) = 4x + 7.$ And when reflecting it on the [vertical] axis, I did $f(-x) = -4x + 7.$
After that we translate it to the left by $2,$ therefore the equation becomes $f(-x- 2) = -4(x + 2) + 7$ or $-4x - 1.$
And then we multiply it by $-1$ (reflecting it on the [horizontal] axis) and get $4x + 1,$ and then take away $3$ (to translate it down by $3$ units). Thus, we get $4x - 2.$

Rishik K used systematic trial and error to try all of the possible sequences of transformations. Rishik began by showing what each transofrmation does algebraically, which Ci Hui included at the end of their solution. This is Rishik K's work:

I decided to use trial and error to solve this problem. Trial and error may be the most effective because it allows us to go through all the combinations and find out all the possible orders and solutions, without the risk of skipping any. It may be easier to use this method rather than attempting this graphically because we may have some messy graphs with 24 lines but it is still possible. 
We can do this by numbering each transformation, so in this case we could take:

1     Translate down by 3 units -> subtract 3 form the y-intercept
2     Translate left by 2 units -> substitute x with x+2
3     Reflect in vertical axis -> multiply gradient by -1
4     Reflect in horizontal axis -> multiply whole equation by -1

4! = 1$\times$2$\times$3$\times$4 = 24 which meant that I completed 24 attempts. After that, I found 5 possible orders starting at ($y = 4x + 7$) and successfully finishing at ($y = 4x – 2$).

These 5 possible orders were:

• 3241    Also found by Lynn
• 3421    Also found by Miraya and Ci Hui
• 4132    
• 4312    Also found by Miraya
• 4321    Also found by Miraya and Ci Hui

 
Reasons for multiple answers and orders:

• In some cases, I had obtained $4x+1$ and $-4x-1$ and $4x – 1$
• Especially using transformation 3 and 4 which is the reflection, we could manipulate theses expressions ($4x+1, -4x-1, 4x-1$) using the multiplication by $-1$ to obtain the same expressions, therefore in the end get the same answer.
• In other instances, I found some expressions like $4x-10$ and $4x-7$ and $-4x-7$ floating around but in different orders they all appeared to produce the same output of $4x-2.$
• Also, I believe that another important thing is the transformation of left by $2$ units because this can be also interpreted as substitute $x$ with $x+2$ in the expression. This $x+2$ has led to many expressions turning out to be similar. 
• Additionally, I realised that if $1,2,7,10$ was floating around in the expression it is most likely going to end up as $4x – 2$ but this may not always be true.

Rishik has found a lot of solutions, but we know Rishik didn't find all of them, because one of Miraya's solutions is not on Rishik's list.

Miraya and Ci Hui noticed that the two reflections, when applied one after the other, have the same effect, regardless of which reflection comes first. Are there any other pairs of transformations for which this is true? Can this help group transformation sequences into families that produce the same result?

Jack from Hertford South Primary used the same approach as Rishik K. This is Jack's table, which shows all the possibilities:

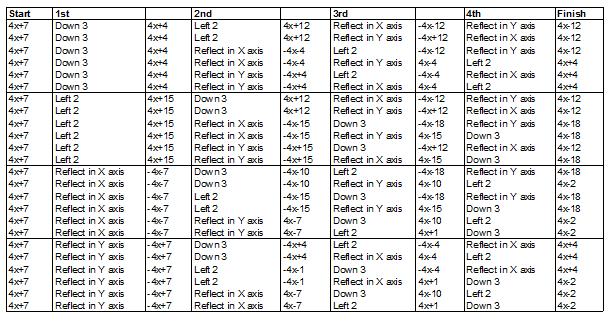
So there are 24 orders of 4 transformations, and only 4 possible finishing graphs. There are 6 ways to make $y=4x-12$, 6 ways to make $y=4x+4$, 6 ways to make $y=4x-18$ and 6 ways to make what we were looking for $y=4x-2$.